
【题目】在平面直角坐标系xOy中,直线L:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数![]() (x>0)的图象的交点P位于第一象限.
(x>0)的图象的交点P位于第一象限.
(1)若点P的坐标为(1,6),
①求m的值及点A的坐标;
②![]() =_________;
=_________;
(2)直线h:y=2kx-2与y轴交于点C,与直线L1交于点Q,若点P的横坐标为1,
①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围.
【答案】(1)①6;(2,0)②![]() ;(2)①P(1,3k)②m≥3
;(2)①P(1,3k)②m≥3
【解析】
(1)①把P(1,6)代入函数![]() (x>0)即可求得m的值,直线l1:y=kx+2k(k>0)中,令y=0,即可求得x的值,从而求得A的坐标;
(x>0)即可求得m的值,直线l1:y=kx+2k(k>0)中,令y=0,即可求得x的值,从而求得A的坐标;
②把P的坐标代入y=kx+2k即可求得k的值,进而求得B的坐标,然后根据勾股定理求得PB和PA,即可求得![]() 的值;
的值;
(2)①把x=1代入y=kx+2k,求得y=3k,即可求得P(1,3k);
②分别过点P、Q作PM⊥x轴于M,QN⊥x轴于N,则点M、点N的横坐标1,2+![]() ,若PQ=PA,则
,若PQ=PA,则![]() =1,根据平行线分线段成比例定理则
=1,根据平行线分线段成比例定理则![]() =
=![]() =1,得出MN=MA=3,即可得到2+
=1,得出MN=MA=3,即可得到2+![]() 1=3,解得k=1,根据题意即可得到当
1=3,解得k=1,根据题意即可得到当![]() =
=![]() ≤1时,k≥1,则m=3k≥3.
≤1时,k≥1,则m=3k≥3.
(1)①令y=0,则kx+2k=0,
∵k>0,解得x=2,
∴点A的坐标为(2,0),
∵点P的坐标为(1,6),
∴m=1×6=6;
②∵直线l1:y=kx+2k(k>0)函数![]() (x>0)的图象的交点P,且P(1,6),
(x>0)的图象的交点P,且P(1,6),
∴6=k+2k,解得k=2,
∴y=2x+4,
令x=0,则y=4,
∴B(0,4),
∵点A的坐标为(2,0),
∴PA=![]() ,PB=
,PB=![]() ,
,
∴![]() =
=![]() ,
,
故答案为![]() ;
;
(2)①把x=1代入y=kx+2k得y=3k,
∴P(1,3k);
②由题意得,kx+2k=2kx2,
解得x=2+![]() ,
,
∴点Q的横坐标为2+![]() ,
,
∵2+![]() >1(k>0),
>1(k>0),
∴点Q在点P的右侧,
如图,分别过点P、Q作PM⊥x轴于M,QN⊥x轴于N,则点M、点N的横坐标为1,2+![]() ,
,
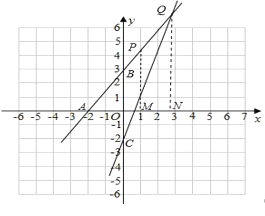
若PQ=PA,则![]() =1,
=1,
∴![]() =
=![]() =1,
=1,
∴MN=MA,
∴2+![]() 1=3,解得k=1,
1=3,解得k=1,
∵MA=3,
∴当![]() =
=![]() ≤1时,k≥1,
≤1时,k≥1,
∴m=3k≥3,
∴当PQ≤PA时,m≥3.


科目:初中数学 来源: 题型:
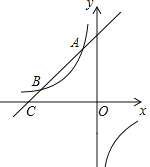
【题目】如图,一次函数y=x+b的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a)、B两点,与x轴交于点C(﹣4,0).
(k为常数且k≠0)的图象交于A(﹣1,a)、B两点,与x轴交于点C(﹣4,0).
(1)求一次函数和反比例函数的表达式;
(2)若点D是第四象限内反比例函数图象上的点,且点D到直线AC的距离为5![]() ,求点D的横坐标.
,求点D的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了调查同学们对学生会的满意度,随机抽取了部分同学作问卷调查:用“![]() ”表示“相 当满意”,“
”表示“相 当满意”,“![]() ”表示“满意”,“
”表示“满意”,“![]() ”表示“比较满意”,“
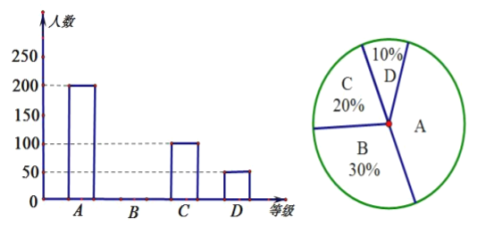
”表示“比较满意”,“![]() ”表示“不满意”,下图是负责 调查同学根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
”表示“不满意”,下图是负责 调查同学根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少人;
(2)通过计算补全条形图;
(3)如果该学校有![]() 名学生,请你估计该校学生对学生会感到“相当满意”的约有多少人?
名学生,请你估计该校学生对学生会感到“相当满意”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
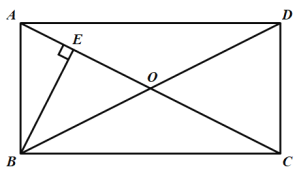
【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O作BD的垂线与边AD,BC分别交于点E,F,连接BE交AC于点K,连接DF.
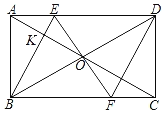
(1)求证:四边形EBFD是菱形;
(2)若BK=3EK,AE=4,求四边形EBFD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
(1)求证:![]() ABCD是矩形;
ABCD是矩形;
(2)若AD=![]() ,cos∠ABE=
,cos∠ABE=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
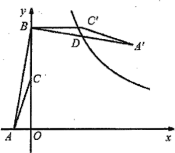
【题目】如图,点![]() 的坐标是(-1,0),点
的坐标是(-1,0),点![]() 的坐标是(0,6),
的坐标是(0,6),![]() 为
为![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 逆时针旋转90°.后得到
逆时针旋转90°.后得到![]() .若反比例函数
.若反比例函数![]() 的图像恰好经过
的图像恰好经过![]() 的中点
的中点![]() ,则k的值是( )
,则k的值是( )
A.19B.16.5C.14D.11.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于两点
的图像交于两点![]() ,
,![]() .
.
(1)求反比例函数与一次函数的函数表达式;
(2)在反比例函数的图像上找点![]() ,使得点
,使得点![]() 构成以
构成以![]() 为底的等腰三角形,请求出所有满足条件的点
为底的等腰三角形,请求出所有满足条件的点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球已经进入大数据时代,大数据(bigdata)是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值.为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是根据调查结果绘制出不完整的两个统计图表:
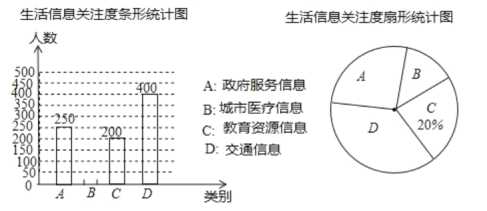
请根据图中提供的信息,解答下列问题:
(1)本次参与调查的人数是________,扇形统计图中![]() 部分的圆心角的度数是________,并补全条形统计图;
部分的圆心角的度数是________,并补全条形统计图;
(2)这次调查的市民最关心的四类生活信息的众数是________类;
(3)若我市现有常住人口约600万,请你估计最关心“城市医疗信息”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的任意一点
中的任意一点![]() ,给出如下定义:经过点
,给出如下定义:经过点![]() 且平行于两坐标轴夹角平分线的直线,叫做点
且平行于两坐标轴夹角平分线的直线,叫做点![]() 的“特征线”.例如:点
的“特征线”.例如:点![]() 的特征线是
的特征线是![]() 和
和![]() .
.
(1)若点![]() 的其中一条特征线是
的其中一条特征线是![]() ,则在
,则在![]() 、
、![]() 、
、![]() 三个点中,可能是点
三个点中,可能是点![]() 的点有_______;
的点有_______;
(2)已知点![]() 的平行于第二、四象限夹角平分线的特征线与
的平行于第二、四象限夹角平分线的特征线与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .使
.使![]() 的面积不小于6,求
的面积不小于6,求![]() 的取值范围;
的取值范围;
(3)已知点![]() ,
,![]() ,且
,且![]() 的半径为1.当
的半径为1.当![]() 与点
与点![]() 的特征线存在交点时,直接写出
的特征线存在交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com