练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
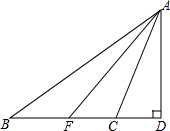
    15．如图所示，AD、AF分别是△ABC的高和角平分线，已知∠B=36°，∠ACB=104°，求∠DAF的度数．

    分析 先根据△ACB中，∠B=36°，∠ACB=104°求出∠BAC的度数，再由AF是∠BAC的角平分线求出∠BAF的度数，再由三角形外角的性质得出∠AFD的度数，由三角形内角和定理即可得出结论．

    解答 解：∵△ACB中，∠B=36°，∠ACB=104°，
    ∴∠BAC=180°-104°-36°=40°．
    ∵AF是∠BAC的角平分线，
    ∴∠BAF=20°，
    ∴∠AFD=∠B+∠BAF=36°+20°=56°．
    在△AFD中，
    ∵AD⊥BD，
    ∴∠D=90°，
    ∴∠DAF=90°-∠AFD=90°-56°=34°．

    点评 本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．某市为处理污水，需要铺设一条长为5000m的管道，为了尽量减少施工对交通所造成的影响，实际施工时每天比原计划多铺设20m，结果提前15天完成任务．设原计划每天铺设管道x m，则可得方程$\frac{5000}{x}$-$\frac{5000}{x+20}$=15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

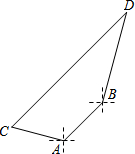    6．在海岸A处，发现北偏东45°方向、距离A处20海里的B处有一艘走私船；在A处北偏西75°方向、距离A处20海里的C处的缉私船奉命以10$\sqrt{3}$海里/小时的速度追截走私船．同时，走私船正以10海里/小时的速度从B处向北偏东15°方向逃窜，问缉私船沿什么方向能最快追上走私船？最少要花多少时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

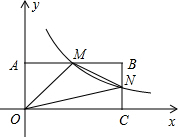    3．如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线y=-$\frac{1}{2}$x+3交AB，BC分别于点M，N，反比例函数y=$\frac{k}{x}$的图象经过点M，N．
    （1）求点M，N的坐标；
    （2）求反比例函数的解析式；
    （3）求四边形BMON的面积S；
    （4）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，直线AB分别交EF、BC于点A、B，AC平分∠BAE，∠ABC=76°，∠GAF=52°，EF与BC平行吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图所示的网格中各有不同的图案，不能通过平移得到的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列计算中，正确的是（　　）
    A．（-5）-（-3）=-8B．（+5）-（3）=2C．（+7）-（+8）=-1D．（-5）-|-5|=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．阅读下面材料，并解答问题．
    材料：将分式$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$拆分成一个整式与一个分式（分子为整数）的和的形式
    解：由于分母为-x2+1，可设-x4-x2+3=（-x2+1）（x2+a）+b
    ∴-x4-x2+3=-x4-ax2+x2+a+b∴-x4-x2+3=-x4-（a-1）x2+（a+b）
    ∵对于任意x，上述等式均成立，∴$\left\{\begin{array}{l}{a-1=1}\\{a+b=3}\end{array}\right.$∴$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$
    ∴$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$=$\frac{（-{x}^{2}+1）（{x}^{2}+2）+1}{-{x}^{2}+1}$=$\frac{（-{x}^{2}+1）（{x}^{2}+2）}{-{x}^{2}+1}$+$\frac{1}{-{x}^{2}+1}$=x2+2+$\frac{1}{-{x}^{2}+1}$
    这样，分式$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$被拆分成了一个整式x2+2与一个分式$\frac{1}{-{x}^{2}+1}$的和
    阅读上面的材料后，请你解答下列问题
    （1）将分式$\frac{{x}^{4}-4{x}^{2}-4}{{x}^{2}+1}$拆分成一个整式与一个分式（分子为整数）的和的形式．
    （2）试说明$\frac{{x}^{4}-4{x}^{2}-4}{{x}^{2}+1}$的最小值为-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．（1）计算：（$\sqrt{3}$）2-$\sqrt{（-1）^{2}}$                   
    （2）解方程：2x2-2x=3．

    查看答案和解析>>

    同步练习册答案