
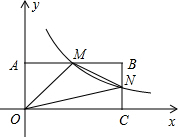
 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.分析 (1)求出OA=BC=2,将y=2代入y=-$\frac{1}{2}$x+3求出x=2,得出M的坐标,进而将x=4代入y=-$\frac{1}{2}$x+3得:y=1,求出N点坐标;
(2)把M的坐标代入反比例函数的解析式即可求出答案;
(3)利用S四边形BMON=S矩形OABC-S△AOM-S△CON,求出即可;
(4)利用(3)中所求,再求出OP的值,即可求出P的坐标.
解答 解:(1)∵B(4,2),四边形OABC是矩形,
∴OA=BC=2,
将y=2代入y=-$\frac{1}{2}$x+3得:x=2,
∴M(2,2),
将x=4代入y=-$\frac{1}{2}$x+3得:y=1,
∴N(4,1);
(2)∵M(2,2),
把M的坐标代入y=$\frac{k}{x}$得:k=4,
∴反比例函数的解析式是y=$\frac{4}{x}$;
(3)由题意可得:S四边形BMON=S矩形OABC-S△AOM-S△CON
=4×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×4×1
=4;
(4)由(3)得,$\frac{1}{2}$OP×AM=4,
∵AM=2,
∴OP=4,
∴点P的坐标是(0,4)或(0,-4).
点评 本题考查了用待定系数法求反比例函数的解析式,一次函数与反比例函数的交点问题,三角形的面积,矩形的性质等知识点的应用,注意分类讨论得出P点坐标是解题关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
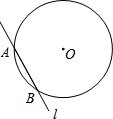 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为( )
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{π}{2}$+$\sqrt{3}$ | D. | $\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
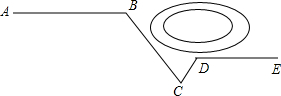 如图,煤气公司安装煤气管道,他们从点A处铺设到点B处时,由于有一个人工湖挡住了去路,需要改变方向经过点C,再拐到点D,然后沿与AB平行的DE方向继续铺设.如图∠BCD=50°,∠ABC=120°,求∠CDE的大小.
如图,煤气公司安装煤气管道,他们从点A处铺设到点B处时,由于有一个人工湖挡住了去路,需要改变方向经过点C,再拐到点D,然后沿与AB平行的DE方向继续铺设.如图∠BCD=50°,∠ABC=120°,求∠CDE的大小.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b | B. | b>a | C. | a≥b | D. | b≥a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com