
| 名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
| 图形 | 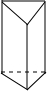 | 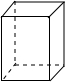 | 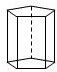 | 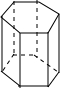 |
| 顶点数a | 6 | 8 | 10 | 12 |
| 棱数b | 9 | 12 | 15 | 18 |
| 面数c | 5 | 6 | 7 | 8 |
分析 结合三棱柱、四棱柱和五棱柱的特点,即可填表:
(1)(2)(3)根据已知的面、顶点和棱与几棱柱的关系,可知n棱柱一定有(n+2)个面,2n个顶点和3n条棱,进而得出答案;
(4)利用前面的规律得出a,b,c之间的关系.
解答 解:填表如下:
| 名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
| 图形 |  |  |  |  |
| 顶点数a | 6 | 8 | 10 | 12 |
| 棱数b | 9 | 12 | 15 | 18 |
| 面数c | 5 | 6 | 7 | 8 |
点评 此题主要考查了欧拉公式,熟记常见棱柱的特征,可以总结一般规律:n棱柱有(n+2)个面,2n个顶点和3n条棱是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | (a-1b2)3=$\frac{{b}^{6}}{{a}^{3}}$ | B. | (a2b-2)-3=$\frac{{b}^{6}}{{a}^{6}}$ | ||
| C. | (-3ab-1)3=-$\frac{{a}^{3}}{27{b}^{3}}$ | D. | (2m2n-2)2•3m-3n3=$\frac{12m}{n}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
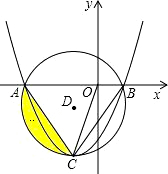 已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-3,-3)为圆心,6为半径的圆上,且经过⊙D与x轴的两个交点A、B,连结AC、BC、OC.
已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-3,-3)为圆心,6为半径的圆上,且经过⊙D与x轴的两个交点A、B,连结AC、BC、OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
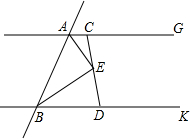 如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.
如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
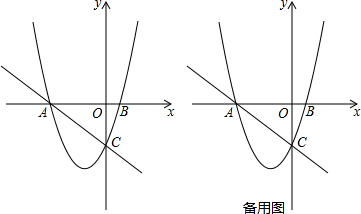
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
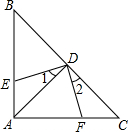 如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF,若AB=8cm,则四边形AEDF的面积为( )
如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF,若AB=8cm,则四边形AEDF的面积为( )| A. | 64 | B. | 32 | C. | 16 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a∥b,b∥c,那么a∥c | |
| B. | 直角三角形的两个锐角互余 | |
| C. | 两条直线被第三条直线所截,内错角相等 | |
| D. | 两点之间,线段最短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com