
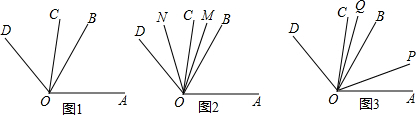
分析 (1)根据角度的和、差即可求解;
(2)根据(1)以及∠AOD=4∠BOC即可列方程求解;
(3)根据∠MON=$\frac{1}{2}$(∠AOD-∠COD)-$\frac{1}{2}$∠AOC,求得∠MON的度数,即可判断;
(4)设运动的时间是t秒,则∠POB=(80-m)-10t,∠QOB=m-5t,根据PB=2BQ即可列方程求解.
解答 解:(1)∠COD=∠BOD-∠BOC=(80-m)°,
∠AOD=∠COD+∠AOC=80-m+80=160-m°;
故答案是:80-m,160-m;
(2)∵∠AOD=4∠BOC,
∴160-m=4m,
解得:m=32;
(3)∠MON是定值.
理由是:∵OM、ON是∠AOD和∠COD的平分线,
∴∠MOD=$\frac{1}{2}$∠AOD,∠NOD=$\frac{1}{2}$∠COD,
∴∠MON=$\frac{1}{2}$(∠AOD-∠COD)-$\frac{1}{2}$∠AOC=40°,
∴∠MON的度数是定值,是40°;
(4)设运动的时间是t秒,则∠POB=(80-m)-10t,∠QOB=m-5t,
∵PB=2BQ,
∴(80-m)-10t=2(m-5t),
∴m=$\frac{80}{3}$.
点评 本题考查了角度的计算,求角度的方法一般是转化为角的和、差计算.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
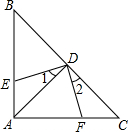 如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF,若AB=8cm,则四边形AEDF的面积为( )
如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF,若AB=8cm,则四边形AEDF的面积为( )| A. | 64 | B. | 32 | C. | 16 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a∥b,b∥c,那么a∥c | |
| B. | 直角三角形的两个锐角互余 | |
| C. | 两条直线被第三条直线所截,内错角相等 | |
| D. | 两点之间,线段最短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com