
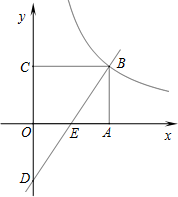 矩形ABCO如图放置,点A,C在坐标轴上,点B在第一象限,一次函数y=kx-3的图象过点B,分别交x轴、y轴于点E、D,已知C(0,3)且S△BCD=12.
矩形ABCO如图放置,点A,C在坐标轴上,点B在第一象限,一次函数y=kx-3的图象过点B,分别交x轴、y轴于点E、D,已知C(0,3)且S△BCD=12.分析 (1)根据题意求得点D的坐标,所以由矩形的性质和三角形的面积公式可以求得点B的坐标,把点B的坐标代入一次函数解析式,求得k的值即可;
(2)把点B的坐标代入反比例函数$y=\frac{m}{x}$得到m的值,即该反比例函数的解析式;然后结合三角形的面积公式来求点P的坐标;
(3)当反比例函数图象经过点B时,m最大;当反比例函数图象与直线AC有一个交点时,m最小.
解答 解:(1)∵一次函数y=kx-3的图象交y轴于点D,
∴D(0,-3).
∵点C(0,3)
∴CD=6.
又∵四边形ABCO为矩形,
∴BC⊥CD
S△BCD=$\frac{1}{2}$CD.BC=12,
∴BC=4
∴B(4,3).
把点B(4,3)代入y=kx-3得:k=$\frac{3}{2}$,
∴y=$\frac{3}{2}$x-3;
(2)∵反比例函数$y=\frac{m}{x}$过B(4,3),
∴m=12,
∴y=$\frac{12}{x}$,
∵直线y=$\frac{3}{2}$x-3过x轴上的E点.
∴当y=0时,x=2,
∴E(2,0),S△DOE=$\frac{1}{2}$×2×3=3,
当S△CBP=$\frac{2}{3}$S△DOE时,$\frac{1}{2}$×4×h=$\frac{2}{3}$×3
∴h=1.
当点P在直线BC上方时,$\frac{12}{x}$=4,
解得x=3
∴P(3,4).
同理当点P在直线BC下方时点P(6,2).
综上所述,符合条件的点P的坐标是(3,4)或(6,2).
(3)m的取值范围是3<m<12.
点评 本题考查了反比例函数与一次函数的交点问题.解答(2)题时,要注意点P的位置有2个.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
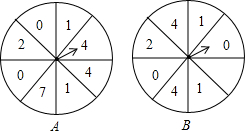 某天,小明和小华利用“争1点”的游戏来预测一场足球比赛的冠军.如图,两个可以自由转动的转盘A,B,每个转盘被分成8个相等的扇形,其规则如下:①小明自由转动转盘A,同时小华自由转动转盘B;②转盘停止后,指针指向几就顺时针走几格,得到一个数字(若转盘A中指针指向2,则按顺时针方向走2格得到数字1);③若最终得到的数字是1,则自己所支持的球队称为预测冠军(若双方都得到1,则重新开始).这个游戏对双方公平吗?请说明理由.
某天,小明和小华利用“争1点”的游戏来预测一场足球比赛的冠军.如图,两个可以自由转动的转盘A,B,每个转盘被分成8个相等的扇形,其规则如下:①小明自由转动转盘A,同时小华自由转动转盘B;②转盘停止后,指针指向几就顺时针走几格,得到一个数字(若转盘A中指针指向2,则按顺时针方向走2格得到数字1);③若最终得到的数字是1,则自己所支持的球队称为预测冠军(若双方都得到1,则重新开始).这个游戏对双方公平吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
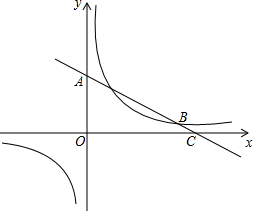 如图,在平面直角坐标系中,点A(0,5),C(10,0)在一次函数y=kx+b(b≠0)的图象上,与反比例函数y=$\frac{k′}{x}$(k′≠0)交于点B(8,t).
如图,在平面直角坐标系中,点A(0,5),C(10,0)在一次函数y=kx+b(b≠0)的图象上,与反比例函数y=$\frac{k′}{x}$(k′≠0)交于点B(8,t).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
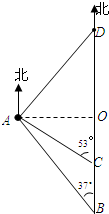 如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
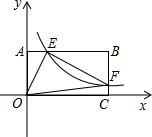 如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=$\frac{k}{x}$(x>0)的图象与边BC交与点F.
如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=$\frac{k}{x}$(x>0)的图象与边BC交与点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
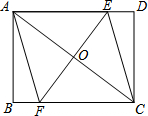 如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE.
如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.365×1012元 | B. | 13.65×1012元 | C. | 1.365×1013元 | D. | 0.1365×1014元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com