
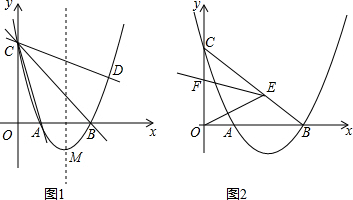
���� ��1�����ö���ʽ������֪����������������н�����⼴�ɣ�
��2����C��B��������겻���жϳ�OB=OC������CBO=45�㣬��ô��ȡBN��x�ύCD��N����ϡ�ֱ��CD��ֱ��CA����ֱ��CB�Գơ��ɵó�A��N����ֱ��BC�Գƣ���ϵ�B�������Լ�AB�ij����ɵõ���N�����꣬����ȷC��N�������������£�ֱ��CD�Ľ���ʽ�����ɴ���ϵ������ã�
��4���������P�����꣬��M��B��C����������֪�����ɵõ�PM2��PB2��PC2�ı���ʽ�������ɵ���֪�������������P�����꣬�Ӷ���һ���жϳ�ֱ��OP�������ߵĽ��������
��� �⣺��1���������ߵĽ���ʽΪ��Y=a��x-2��2-1��
�ߵ�B��3��0�����������ϣ���0=a��3-2��2-1��
��ã�a=1��
��������ߵĽ���ʽΪ��y=��x-2��2-1����y=x2-4x+3��
��2����y=x2-4x+3����x=0����y=3��
��C��0��3����
��OB=OC=3��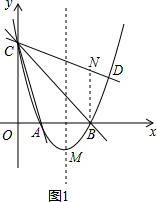
���ABC=45�㣮
����B��BN��x�ύCD�ڵ�N����ͼ1�������ABC=��NBC=45�㣮
��ֱ��CD��ֱ��CA����ֱ��BC�Գƣ�
���ACB=��NCB��
�ڡ�ACB�͡�NCB��
$\left\{\begin{array}{l}{��NCB=��ACB}\\{CB=CB}\\{��NBC=��ABC}\end{array}\right.$��
���ACB�ա�NCB��ASA����
��BN=BA��
��A��B���������ߵĶԳ���x=2�Գƣ�B��3��0����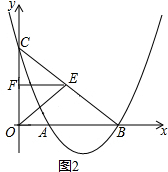
��A��1��0������BN=BA=2����N��3��2����
��ֱ��CD�Ľ���ʽΪ��y=kx+3��
��2=3k+3��
��ã�k=-$\frac{1}{3}$��
��ֱ��CD�Ľ���ʽΪ��y=-$\frac{1}{3}$x+3��
��3����EF=OFʱ��E��$\frac{3}{2}$��$\frac{3}{2}$����
��OE=EFʱ��֤����OBE�ա�ECF��E��$\frac{3\sqrt{2}}{2}$��$\frac{6-3\sqrt{2}}{2}$����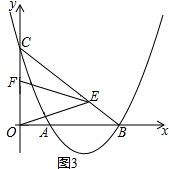
��4����P��2��p������M��2��-1����B��3��0����C��0��3����
����ݹ��ɶ�������PM2=��p+1��2=p2+2p+1��PB2=��3-2��2+p2=p2+1��
PC2=22+��p-3��2=p2-6p+13��
��PM2+PB2+PC2=35��
��p2+2p+1+p2-6p+13=35��
��������3p2-4p-20=0��
��ã�p1=-2��p2=$\frac{10}{3}$��
��P��2��-2����2��$\frac{10}{3}$����
��P��2��$\frac{10}{3}$��ʱ��ֱ��OP��y=$\frac{5}{3}$x�����������ߵĽ���ʽ�У�$\frac{5}{3}$x=x2-4x+3��
��á���0�������������2�����㣻
��P��2��-2��ʱ��ֱ��OP��y=-x�����������ߵĽ���ʽ�У�
x2-4x+3=-x���� x2-3x+3=0
��=��-3��2-4��3��0��
�ʸ�ֱ����������û�н��㣻
���ϣ���P��2��$\frac{10}{3}$��ʱ��ֱ��OP�����������������㣻��P��2��-2��ʱ��ֱ��OP��������û�н��㣮
���� ������κ����ۺ��⿼������ݽ�Ϊ��������Ҫ�漰������������ʽ��ȷ������Գ�ͼ�ε����ʡ�����ϵ�����ľ��빫ʽ�Լ�����ͼ�ν����������֪ʶ�����ػ������ݵĿ��飮


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ڢۢ� | B�� | �٢ۢ� | C�� | �٢� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | �� | -m2-1 | 2 | 3 | �� |
| y | �� | -1 | 0 | n2+1 | �� |
| A�� | x��2 | B�� | x��3 | C�� | x��2 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�콭��ʡ���Ƹ��й�������Ƭ���꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ���ѡ��
��ͼ����D��0��3����O��0��0����C��4��0���ڡ�A�ϣ�BD�ǡ�A��һ���ң���sin��OBD=��������
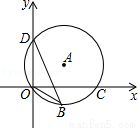
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��1����һ�ȴ�����ֱ����OM��OP��AC�dz��Ȳ���Ļ���֧�ܣ�����һ�˹̶��ڴ����ĵ�A������һ�����߶�OP�ϻ�����������OM��ͼʾ����������ת45�㵽��ONλ�ã���ͼ��2������ʱ����A��C�Ķ�Ӧλ�÷ֱ��ǵ�B��D����������ODBΪ37�㣬��D����O�ľ���Ϊ28cm��
��ͼ��1����һ�ȴ�����ֱ����OM��OP��AC�dz��Ȳ���Ļ���֧�ܣ�����һ�˹̶��ڴ����ĵ�A������һ�����߶�OP�ϻ�����������OM��ͼʾ����������ת45�㵽��ONλ�ã���ͼ��2������ʱ����A��C�Ķ�Ӧλ�÷ֱ��ǵ�B��D����������ODBΪ37�㣬��D����O�ľ���Ϊ28cm���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com