
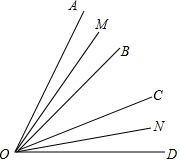
 如图,OB、OC是∠AOD的两条射线,OM和ON分别是∠AOB和∠COD内部的一条射线,且∠AOD=α,∠MON=β.
如图,OB、OC是∠AOD的两条射线,OM和ON分别是∠AOB和∠COD内部的一条射线,且∠AOD=α,∠MON=β.分析 (1)根据∠BOC=∠MON-∠BOM-∠CON,等量代换即可表示出∠BOC的大小;
(2)①当∠AOM=2∠BOM,∠DON=2∠CON时,等量代换即可表示出∠BOC的大小;②当∠AOM=3∠BOM,∠DON=3∠CON时,等量代换即可表示出∠BOC的大小;
(3)当∠AOM=n∠BOM,∠DON=n∠CON时,等量代换即可表示出∠BOC的大小;
解答 (1)∵∠AOM=∠BOM=$\frac{1}{2}$∠AOB,∠CON=∠DON=$\frac{1}{2}$∠COD,
∵∠BOC=∠MON-∠BOM-∠CON=∠MON-$\frac{1}{2}$∠AOB-$\frac{1}{2}$∠COD=∠MON-$\frac{1}{2}$(∠AOB+∠COD)=∠MON-$\frac{1}{2}$(∠AOD-∠BOC)=β-$\frac{1}{2}$(α-∠BOC)=β-$\frac{1}{2}$α+$\frac{1}{2}$∠BOC,
则∠BOC=2β-α.
(2)①当∠AOM=2∠BOM,∠DON=2∠CON时,
∵∠BOM+∠CON=$\frac{1}{2}$(∠AOM+∠DON)=$\frac{1}{2}$(α-β),
∴∠BOC=∠MON-(∠BOM+∠CON)=β-$\frac{1}{2}$(α-β)=$\frac{3}{2}$β-$\frac{1}{2}$α;
②当∠AOM=3∠BOM,∠DON=3∠CON时,
∵∠BOM+∠CON=$\frac{1}{3}$(∠AOM+∠DON)=$\frac{1}{3}$(α-β),
∴∠BOC=∠MON-(∠BOM+∠CON)=β-$\frac{1}{3}$(α-β)=$\frac{4}{3}$β-$\frac{1}{3}$α;
(3)当∠AOM=n∠BOM,∠DON=n∠CON时,
∵∠BOM+∠CON=$\frac{1}{n}$(∠AOM+∠DON)=$\frac{1}{n}$(α-β),
∴∠BOC=∠MON-(∠BOM+∠CON)=β-$\frac{1}{n}$(α-β)=$\frac{n+1}{n}$β-$\frac{1}{n}$α;
故答案为:$\frac{n+1}{n}$β-$\frac{1}{n}$α.
点评 此题考查了角的计算,以及角平分线定义,利用了等量代换的思想,熟练掌握角平分线定义是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2998 | B. | 3001 | C. | 3002 | D. | 3005 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
| 方程有两个 不相等的负实根 | 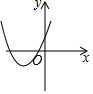 | $\left\{\begin{array}{l}a>0\\△={b^2}-4ac>0\\-\frac{b}{2a}<0\\ c>0.\end{array}\right.$ |
| 方程有一个负实根,一个正实根 | 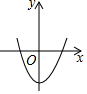 | $\left\{\begin{array}{l}a>0\\ c<0.\end{array}\right.$ |
| 方程有两个 不相等的正实根 | 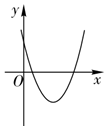 | $\left\{\begin{array}{l}a>0\\△={b^2}-4ac>0\\-\frac{b}{2a}>0\\ c>0.\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.1(精确到0.1) | B. | 0.05(精确到0.01) | ||
| C. | 0.05(精确到0.001) | D. | 0.0503(精确到0.0001) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com