
分析 首先应用平方差公式,可得(x-2-y-2)=(x-1+y-1)(x-1-y-1),据此推得(x-1+y-1)÷(x-2-y-2)=$\frac{1}{{x}^{-1}{-y}^{-1}}$;然后根据负整数指数幂的运算方法,求出算式的值是多少即可.
解答 解:(x-1+y-1)÷(x-2-y-2)
=(x-1+y-1)÷[(x-1+y-1)(x-1-y-1)]
=$\frac{1}{{x}^{-1}{-y}^{-1}}$
=$\frac{1}{\frac{1}{x}-\frac{1}{y}}$
=$\frac{xy}{y-x}$
点评 此题主要考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
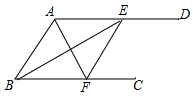 如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证:
如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
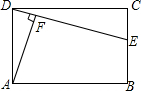 如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.
如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
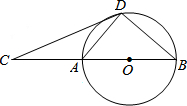 如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com