
���� ��1�����ݡ����¶��κ������Ķ��壬�ɵô𰸣�
��2���ٽⷽ��x2+4x+3=0���ɵú�����x��Ľ���ĺ����꣬�����ɵô𰸣��ڸ��ݡ����¶��κ��������������꣬����⣻
��3�����ݡ����¶��κ������Ķ����ڶԷ���ͼ���ϣ��г���Ԫһ�η����飬�������Ⲣ�ҽⷽ���飬�ɵô𰸣�
��� �⣺��1��һ�����κ����ġ����¶��κ���������������
�ʴ�Ϊ������
��2������y=0����x2+4x+3=0��
��ã�x1=-1��x2=-3��
���Զ��κ���y=x2+4x+3��x��Ľ�������Ϊ��-3��0������-1��0����
�ڡ�y=x2+4x+3=��x+2��2-1��
�ඥ������Ϊ��-2��-1����
���ԣ�-3��0��Ϊ�����Ҿ�����-2��-1���������ߵĺ�����ϵʽΪ
y=a��x+3��2��
��x=-2��y=-1����y=a��x+3��2�����a=-1��
����κ���y=x2+4x+3��һ�������¶��κ�����Ϊy=-��x+3��2=-x2-6x-9��
ͬ�������ԣ�-1��0��Ϊ�����Ҿ�����-2��-1���������ߵĺ�����ϵʽ��
�����κ���y=x2+4x+3����һ�������¶��κ�����Ϊy=-��x+1��2=-x2-2x-1��
��3��a1=-a2���������£�
��y=a1��x+m��2+n���䶥��Ϊ��-m��n����y=a2��x+h��2+k���䶥��Ϊ��-h��k����
�߶��κ���y1=a1x2+b1x+c1������¶��κ���y2=a2x2+b2x+c2�Ķ��㲻�غϣ�
��m=hʱn��k����n=kʱm��h����m��h��n��k��
���ݡ����¶��κ���������ɵ�
$\left\{\begin{array}{l}{k={a}_{1}��-h+m��^{2}+n}\\{n={a}_{2}��-m+h��^{2}+k}\end{array}\right.$��
�൱m=hʱn=k��n=kʱm=h��
��m��h��n��k��
��a1��-h+m��2=-a2��-m+h��2��m��h��
��a1=-a2��
���� ���⿼���˶��κ��������ʣ����⡰���¶��κ������Ķ����ڶԷ���ͼ�����ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
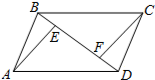 ��ͼ��AB��CD��BC��AD��AB=CD��BE=DF��ͼ��ȫ�ȵ������εĶ����ǣ�������
��ͼ��AB��CD��BC��AD��AB=CD��BE=DF��ͼ��ȫ�ȵ������εĶ����ǣ�������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ������������֤�����̣�����ÿ�������������д�ò����������ݣ�
�Ķ������������֤�����̣�����ÿ�������������д�ò����������ݣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -x6 | B�� | x6 | C�� | -x5 | D�� | x5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 0 | C�� | 9 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com