
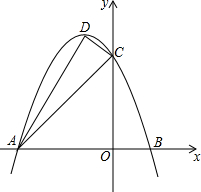
 如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.
如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.分析 (1)根据待定系数法,可得函数解析式;
(2)根据勾股定理,可得AC,CD,AD的长,根据勾股定理的逆定理,可得答案;
(3)分类讨论:①平行四边形AQBP,根据平行四边形的对角线互相平分,可得答案;
②?ABQP,根据平行四边形的对边相等,可得P点的横坐标,根据自变量与函数值的对应关系,可得P点坐标;
③?ABPQ,根据平行四边形的对边相等,可得P点的横坐标,根据自变量与函数值的对应关系,可得P点坐标.
解答 解:(1)当x=0时,y=3,即C(0,3)
将A、C、B点坐标代入、及对称轴,得
$\left\{\begin{array}{l}{9a-3b+c=0}\\{a+b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
抛物线的解析式y=-x2-2x+3;
(2)∵y=-x2-2x+3=-(x-1)2+4,得顶点坐标是(-1,4),
由勾股定理,得
AC2=32+(0-3)2=18,
CD2=(0+1)2+(3-4)2=2,
AD2=(-1+3)2+((4-0)2=20,
AC2+CD2=AD2,
∴△ACD是直角三角形,
S△ACD=$\frac{1}{2}$AC•CD=$\frac{1}{2}$×$\sqrt{18}$×$\sqrt{2}$=3;
(3)①如图1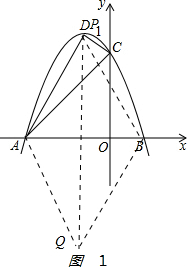 ,
,
平行四边形AQBP,由对角线互相平分,得P1(-1,4),Q(-1,-4);
②如图2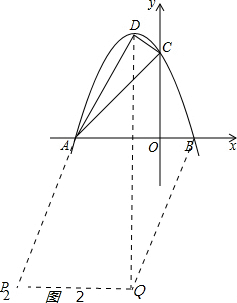 ,
,
?ABQP,PQ=AB=4,-1-4=-5,
当x=-5时,y=-25+10+3=-12,即P2(-5,-12);
③如图3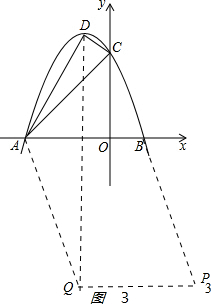 ,
,
?ABPQ,PQ=AB=4,P点的横坐标为-1+4=3,
当x=3时,y=-9-6+3=-12,即P3(3,-12),
综上所述:P1(-1,4),P2(-5,-12),P3(3,-12).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,利用勾股定理、勾股定理的逆定理求三角形的形状;利用平行四边形的性质:对角线互相平分,对边相等是求P点的关键.


科目:初中数学 来源: 题型:解答题
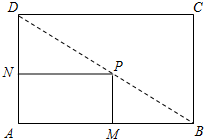 如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).
如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
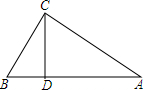 如图,D为△ABC边AB上一点,且CD分△ABC为两个相似比为1:$\sqrt{3}$的一对相似三角形;(不妨如图假设左小右大),求:
如图,D为△ABC边AB上一点,且CD分△ABC为两个相似比为1:$\sqrt{3}$的一对相似三角形;(不妨如图假设左小右大),求:查看答案和解析>>
科目:初中数学 来源:2017届江苏省连云港市灌云县西片九年级下学期第一次月考数学试卷(解析版) 题型:判断题
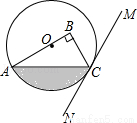
如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com