
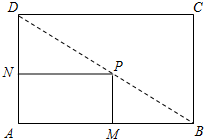
 如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).
如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).分析 (1)由矩形的性质得出PN∥AB,PN=AM,由平行线得出△DNP∽△DAB.得出$\frac{DN}{DA}=\frac{NP}{AB}$,即可得出结果.
(2)设花坛AMPN的面积为S,由矩形的面积公式得出S是x的二次函数,把二次函数化成顶点式,即可得出结果.
解答 解:(1)∵四边形AMPN是矩形,
∴PN∥AB,PN=AM,
∴△DNP∽△DAB.
∴$\frac{DN}{DA}=\frac{NP}{AB}$.
∵AB=160,AD=100,AN=x,AM=y,
∴$\frac{100-x}{100}=\frac{y}{160}$.
∴$y=-\frac{8}{5}x+160$.
(2)设花坛AMPN的面积为S,
则$S=xy=x(-\frac{8}{5}x+160)=-\frac{8}{5}{({x-50})^2}+4000$.
∵$-\frac{8}{5}<0$,
∴当x=50时,S有最大值,S最大值=4000.
即当AM=80m,AN=50m时,花坛AMPN的最大面积为4000m2.
点评 本题考查了相似三角形的应用、矩形的性质、二次函数的应用;熟练掌握矩形的性质,证明三角形相似得出比例式是解决问题的关键.


科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:填空题
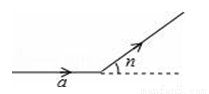
小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=4,n=60,那么机器人回到原点共走了_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
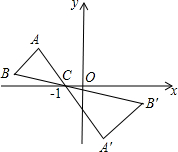 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),则点B的坐标是(-3,$\frac{1}{2}$).
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),则点B的坐标是(-3,$\frac{1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
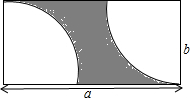 如图所示,阴影部分的面积是(其中a>2b)( )
如图所示,阴影部分的面积是(其中a>2b)( )| A. | ab-$\frac{π{a}^{2}}{4}$ | B. | ab-$\frac{π{b}^{2}}{2}$ | C. | ab-$\frac{π{a}^{2}}{2}$ | D. | ab-$\frac{π{b}^{2}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
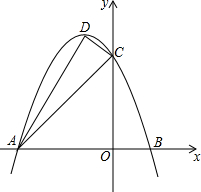 如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.
如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com