
【题目】如图,四棱锥![]() 的底面
的底面![]() 是边长为2的菱形,平面
是边长为2的菱形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
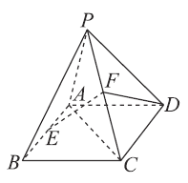
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() ,交
,交![]() 于点
于点![]() ,可证明
,可证明![]() ,
,![]() .从而有
.从而有![]() 平面
平面![]() .
.
同理,![]() 平面
平面![]() .得面面平行后可得线面平行;
.得面面平行后可得线面平行;
(2)以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,写出各点坐标,求出平面
轴建立空间直角坐标系,写出各点坐标,求出平面![]() 的一个法向量,由空间向量法求得线面角的正弦值.
的一个法向量,由空间向量法求得线面角的正弦值.
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
由四边形![]() 是菱形知
是菱形知![]() 是
是![]() 、
、![]() 中点.
中点.
因为![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
同理,![]() 平面
平面![]() .
.
因为![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因为![]() ,
,![]() ,
,![]() 是
是![]() 中点,所以
中点,所以![]() ,
,![]() ,
,
因为平面![]() 平面
平面![]() ,两平面的交线为
,两平面的交线为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 是菱形,边长为2,所以
是菱形,边长为2,所以![]() ,
,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,如图,
轴建立空间直角坐标系,如图,
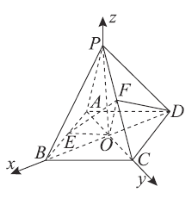
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则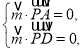
所以![]() ,取
,取![]() ,则
,则![]() ,
,
所以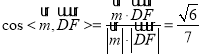 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】某商场推出消费抽现金活动,顾客消费满1000元可以参与一次抽奖,该活动设置了一等奖、二等奖、三等奖以及参与奖,奖金分别为:一等奖200元、二等奖100元、三等奖50元、参与奖20元,具体获奖人数比例分配如图,则下列说法中错误的是( )

A.获得参与奖的人数最多
B.各个奖项中一等奖的总金额最高
C.二等奖获奖人数是一等奖获奖人数的两倍
D.奖金平均数为![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区城乡居民储蓄存款年底余额(单位:亿元)如图所示,下列判断一定不正确的是( )
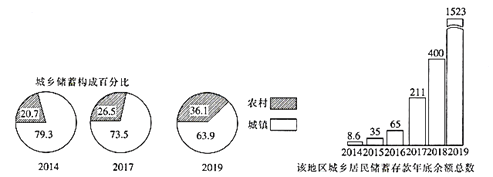
A.城乡居民储蓄存款年底余额逐年增长
B.农村居民的存款年底余额所占比重逐年上升
C.到2019年农村居民存款年底总余额已超过了城镇居民存款年底总余额
D.城镇居民存款年底余额所占的比重逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有四大国粹:京剧、武术、中医和书法.某大学开设这四门课供学生选修,男生甲选其中三门课进行学习,已知他选修了京剧,则他选修书法的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
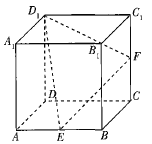
【题目】如图,在棱长为12的正方体![]() 中,已知E,F分别为棱AB,
中,已知E,F分别为棱AB,![]() 的中点,若过点
的中点,若过点![]() ,E,F的平面截正方体
,E,F的平面截正方体![]() 所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面
所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面![]() ,ABCD的交线所成角的余弦值为________.
,ABCD的交线所成角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有教师400人,其中高中教师240人.为了了解该校教师每天课外锻炼时间,现利用分层抽样的方法从该校教师中随机抽取了100名教师进行调查,统计其每天课外锻炼时间(所有教师每天课外锻炼时间均在![]() 分钟内),将统计数据按
分钟内),将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分成6组,制成频率分布直方图如下:假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
分成6组,制成频率分布直方图如下:假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
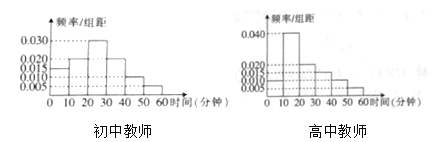
(1)试估计本校教师中缺乏锻炼的人数;
(2)从全市高中教师中随机抽取3人,若![]() 表示每天课外锻炼时间少于10分钟的人数,以这60名高中教师每天课外锻炼时间的频率代替每名高中教师每天课外锻炼时间发生的概率,求随机变量
表示每天课外锻炼时间少于10分钟的人数,以这60名高中教师每天课外锻炼时间的频率代替每名高中教师每天课外锻炼时间发生的概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】角谷猜想,也叫![]() 猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取
猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取![]() ,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若
,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若![]() ,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),与圆
为参数),与圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,
,![]() 为圆
为圆![]() 上的任意一点,求
上的任意一点,求![]() 的最大值.
的最大值.
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,求
两点,求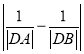 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com