
【题目】选修4一4:坐标系与参数方程
已知在直角坐标系x0y中,曲线![]() :
: (
(![]() 为参数),在以平面直角坐标系的原点)为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系中,曲线
为参数),在以平面直角坐标系的原点)为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 上恰好存在三个不同的点到曲线
上恰好存在三个不同的点到曲线![]() 的距离相等,分别求这三个点的极坐标.
的距离相等,分别求这三个点的极坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() .
.
【解析】
试题分析:(1)先将曲线![]() 的方程平方,利用平方关系,消去参数
的方程平方,利用平方关系,消去参数![]() ,得到曲线
,得到曲线![]() 的普通方程,将曲线
的普通方程,将曲线![]() 的方程利用两角和的正弦公式展开,再利用
的方程利用两角和的正弦公式展开,再利用![]() ,
,![]() 代换,得到曲线
代换,得到曲线![]() 的直角坐标方程;(2)结合(1)知,曲线
的直角坐标方程;(2)结合(1)知,曲线![]() 为圆,曲线
为圆,曲线![]() 为直线,画出图形,通过图形分析得这三个点分别在平行于直线
为直线,画出图形,通过图形分析得这三个点分别在平行于直线![]() 的两条直线
的两条直线![]() ,
,![]() 上,通过直线的位置得到直线
上,通过直线的位置得到直线![]() 和直线
和直线![]() 的方程,再与圆的方程联立,得到三个点
的方程,再与圆的方程联立,得到三个点![]() 、
、![]() 、
、![]() 的坐标.
的坐标.
试题解析:(1)由题意,得![]()
∴曲线![]() 的普通方程为
的普通方程为![]() .
.
∵曲线![]() :
:![]() ,
,
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)∵曲线![]() 为圆
为圆![]() ,圆心
,圆心![]() ,半径为
,半径为![]() ,曲线
,曲线![]() 为直线,∴圆心C1到直线
为直线,∴圆心C1到直线![]() 的距离
的距离![]() ,∵圆
,∵圆![]() 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线![]() 的距离相等,∴这三个点分别在平行于直线
的距离相等,∴这三个点分别在平行于直线![]() 的两条直线
的两条直线![]() ,
,![]() 上,如图所示,
上,如图所示,
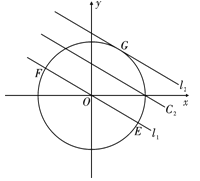
设![]() 与圆
与圆![]() 相交于点E,F,设
相交于点E,F,设![]() 与圆
与圆![]() 相切于点G,
相切于点G,
∴直线![]() ,
,![]() 分别与直线
分别与直线![]() 的距离为
的距离为![]() ,
,
∴![]() :
:![]() ,
,
![]() :
:![]() .
.
由![]() 得
得![]() 或
或![]()
即![]() ,
,![]() ;
;
由![]() 得
得![]() 即
即![]() ,
,
∴E,F,G这三个点的极坐标分别为![]() ,
,![]() ,
,![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】文科做:数列![]() 中,
中,![]() 且满足
且满足![]()
![]()
(I)求数列![]() 的通项公式;
的通项公式;
(II)设![]() ,求
,求![]() ;
;
(III)设![]() =
=![]()
![]() ,是否存在最大的整数
,是否存在最大的整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]()
![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() 的中点.
的中点.

(1)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定点
?若存在,确定点![]() 的位置并证明结论;若不存在,请说明理由.
的位置并证明结论;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理二氧化碳最少为400吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)若该单位每月成本支出不超过105000元,求月处理量的取值范围;
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.问这台机器最佳使用年限是多少年?并求出年平均费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() :
:![]() ,过点
,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,且
,且![]() 在圆
在圆![]() 上.
上.
(1)若直线![]() (
(![]() )经过点
)经过点![]() ,求
,求![]() 的最大值;
的最大值;
(2)求圆![]() 的方程;
的方程;
(3)若过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.![]() 与
与![]() :
:![]() 的交点为
的交点为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)当![]() 时,证明:函数
时,证明:函数![]() 不是奇函数;
不是奇函数;
(2)判断函数![]() 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;
(3)若![]() 是奇函数,且
是奇函数,且![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】面对某种流感病毒,各国医疗科研机构都在研究疫苗,现有A、B、C三个独立的研究机构在一定的时期研制出疫苗的概率分别为![]() .求:
.求:
(1)他们能研制出疫苗的概率;
(2)至多有一个机构研制出疫苗的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆方程;
(2)设不过原点![]() 的直线
的直线![]() ,与该椭圆交于
,与该椭圆交于![]() 两点,直线
两点,直线![]() 的斜率依次为
的斜率依次为![]() ,满足
,满足![]() ,试问:当
,试问:当![]() 变化时,
变化时,![]() 是否为定值?若是,求出此定值,并证明你的结论;若不是请说明理由.
是否为定值?若是,求出此定值,并证明你的结论;若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com