
【题目】已知函数![]() .
.
(1)若函数![]() 的最大值是
的最大值是![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,若存在两个不同的正数
,若存在两个不同的正数![]() ,当函数
,当函数![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)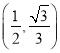
【解析】
(1)对![]() 分类讨论,当
分类讨论,当![]() 时,令
时,令![]() ,根据二次函数的性质计算可得;
,根据二次函数的性质计算可得;
(2)令![]() ,则
,则![]() ,即可判断函数的单调性,函数
,即可判断函数的单调性,函数![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,可转化为函数
,可转化为函数![]() 与
与![]() 有两个正交点
有两个正交点![]() ,即
,即![]() 有两个正根,即
有两个正根,即![]() 有两个大于1的根,再根据一元二次方程的根的分布得到不等式组,即可解得.
有两个大于1的根,再根据一元二次方程的根的分布得到不等式组,即可解得.
解:(1)当![]() 时,
时,![]() ,不合题意;
,不合题意;
![]() 时,令
时,令![]() ,
,
设![]() ,则
,则![]() .
.
①若![]() 开口向上没有最大值,故
开口向上没有最大值,故![]() 无最大值,不合题意;
无最大值,不合题意;
②当![]() 时,且此时对称轴
时,且此时对称轴![]() ,函数
,函数![]() 的最大值是
的最大值是![]() ,
,
所以![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
所以![]() .
.
(2)当![]() 时,设
时,设![]() ,则
,则![]() 的对称轴
的对称轴![]() ,
,
所以当![]() 时
时![]() 为增函数,即
为增函数,即![]() 为增函数.
为增函数.
所以函数![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,
,
可转化为函数![]() 与
与![]() 有两个正交点
有两个正交点![]() ,
,
即![]() 有两个正根.
有两个正根.
即![]() ,设
,设![]() ,
,
所以![]() ,
,
即![]() 有两个大于1的根.
有两个大于1的根.
所以 解得
解得![]() ,
,
所以实数![]() 的取值范围是
的取值范围是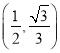 .
.


科目:高中数学 来源: 题型:
【题目】观察下表:
1,2,3,
4,5,6,7,8,
9,10,11,12,13,14,15,
16,17,18,19,20,21,22,23,24,
……
问:(1)此表第![]() 行的第一个数与最后一个数分别是多少?
行的第一个数与最后一个数分别是多少?
(2)此表第![]() 行的各个数之和是多少?
行的各个数之和是多少?
(3)2019是第几行的第几个数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间,某旅行社为吸引中学生去某基地参加夏令营,推出如下收费标准:若夏令营人数不超过30,则每位同学需交费用600元;若夏令营人数超过30,则营员每多1人,每人交费额减少10元(即:营员31人时,每人交费590元,营员32人时,每人交费580元,以此类推),直到达到满额70人为止.
(1)写出夏令营每位同学需交费用![]() (单位:元)与夏令营人数
(单位:元)与夏令营人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当夏令营人数为多少时,旅行社可以获得最大收入?最大收入是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PQ为某公园的一条道路,一半径为20米的圆形观赏鱼塘与PQ相切,记其圆心为O,切点为G.为参观方便,现新修建两条道路CA、CB,分别与圆O相切于D、E两点,同时与PQ分别交于A、B两点,其中C、O、G三点共线且满足CA=CB,记道路CA、CB长之和为![]() .
.
(1)①设∠ACO=![]() ,求出
,求出![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;②设AB=2x米,求出
;②设AB=2x米,求出![]() 关于x的函数关系式
关于x的函数关系式![]() .
.
(2)若新建道路每米造价一定,请选择(1)中的一个函数关系式,研究并确定如何设计使得新建道路造价最少.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求实数![]() 的值;
的值;
(2)当![]() 时,函数
时,函数![]() 存在零点,求实数
存在零点,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若函数
,若函数![]() 与
与![]() 的图像只有一个公共点,求实数
的图像只有一个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:方程![]() 表示焦点在y轴上的椭圆,其离心率的范围是
表示焦点在y轴上的椭圆,其离心率的范围是![]() ,
,
命题q:某人射击,每枪中靶的概率为![]() ,他连续射击两枪至少有一枪中靶的概率超过
,他连续射击两枪至少有一枪中靶的概率超过![]() ,若复合命题:非p为真,p或q为真,求实数
,若复合命题:非p为真,p或q为真,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2010年至2016年生活垃圾无害化处理量(单位:亿吨)的折线图

注:年份代码1~7分别对应年份2010~2016
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请求出相关系数r,并用相关系数的大小说明y与t相关性的强弱;
(2)建立y关于t的回归方程(系数精确到0.01),预测2018年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,![]() ,
, ![]() .
.
参考公式:
相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是中国古代数学名著.书中有如下问题;“今有十等人大官甲等十人.宫赐金依次差降之.上三人先入,得金四斤,持出;下四人后入,得金三斤,持出;中央三人未到者,亦依等次更给.问各得金几何及未到三人复应得金几何.”其意思为:“宫廷依次按照等差数列赏赐甲乙丙丁戊己庚辛壬癸十位官员,前面甲乙丙三人进来,共领到四斤黄金之后,便拿着离开了;接着庚辛壬癸四人共领到三斤黄金后,也拿着离开了;中间丁戊己三人没到,也要按照应分得的数量留给他们.问这十人各得黄金多少,并问没到的三人共应该得到多少黄金.”丁戊己三人共应得黄金的斤数为( )
A.3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com