
【题目】已知函数![]() .
.
(![]() )若
)若![]() ,确定函数
,确定函数![]() 的单调区间.
的单调区间.
(![]() )若
)若![]() ,且对于任意
,且对于任意![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(![]() )求证:不等式
)求证:不等式![]() 对任意正整数
对任意正整数![]() 恒成立.
恒成立.
【答案】(1)![]() 单调增区间为
单调增区间为![]() ,减区间为
,减区间为![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:
(1)求出导函数![]() ,解不等式
,解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;
得减区间;
(2)![]() ,只要
,只要![]() 时,
时, ![]() 恒成立即可,因此利用导数求出
恒成立即可,因此利用导数求出![]() 在
在![]() 上的最小值,由此最小值大于0可得
上的最小值,由此最小值大于0可得![]() 的范围,注意对
的范围,注意对![]() 分类讨论;
分类讨论;
(3)这类证明题一般要利用上面所证函数的结论,由(2)知当![]() 时,
时, ![]() 恒成立,分别取
恒成立,分别取![]() 为
为![]() 可得
可得![]() ,相加同时取
,相加同时取![]() 即证.
即证.
试题解析:
(![]() )
)![]() ,∴
,∴![]() ,
, ![]() ,∴当
,∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴![]() 单调增区间为
单调增区间为![]() ,减区间为
,减区间为![]() .
.
(![]() )
)![]() ,∴
,∴![]() 为偶函数,
为偶函数,
∴![]() 对
对![]() 恒成立,等价于
恒成立,等价于![]() ,对
,对![]() 恒成立,
恒成立,
∴![]() ,解得
,解得![]() ,
,
当![]() 时,
时, ![]() ,在
,在![]() 时成立,
时成立,
∴![]() 在
在![]() 上为增函数,∴
上为增函数,∴![]() ,符合题意,
,符合题意,
当![]() 时,
时, ![]() ,∴
,∴![]() 时,
时, ![]() ,
, ![]() 减,
减,
![]() 时,
时, ![]() ,
, ![]() 增,
增,
∴![]() ,∴
,∴![]() ,综上
,综上![]() .
.
(![]() )证明:由(
)证明:由(![]() )可知,当
)可知,当![]() 时,
时, ![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
![]()
![]()
 ,
,
当![]() 时,
时, ![]() ,得证.
,得证.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的点,
的点, ![]() 垂直于圆
垂直于圆![]() 所在的平面,且
所在的平面,且![]() .
.
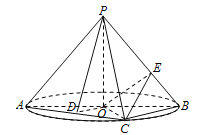
(1)若![]() 为线段
为线段![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 体积的最大值;
体积的最大值;
(3)若![]() ,点
,点![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左右焦点,点
的左右焦点,点![]() 为其上一点,且有
为其上一点,且有![]()
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过
两点,过![]() 与
与![]() 平行的直线
平行的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆内画1条线段,将圆分割成两部分;画2条相交线段,彼此分割成4条线段,将圆分割成4部分;画3条线段,彼此最多分割成9条线段,将圆最多分割成7部分;画4条线段,彼此最多分割成16条线段,将圆最多分割成11部分.那么




(1)在圆内画5条线段,它们彼此最多分割成多少条线段?将圆最多分割成多少部分?
(2)猜想:圆内两两相交的n条线段,彼此最多分割成多少条线段?
(3)猜想:在圆内画n条线段,两两相交,将圆最多分割成多少部分?
并用数学归纳法证明你所得到的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
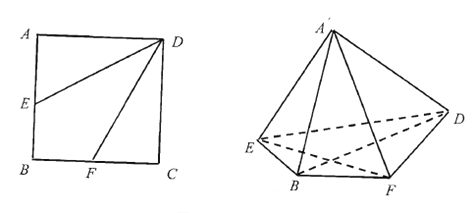
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,将
的中点,将![]() ,
, ![]() ,分别沿
,分别沿![]() ,
, ![]() 折起,使
折起,使![]() ,
, ![]() 两点重合于点
两点重合于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com