
ΓΨΧβΡΩΓΩ¥”Ρ≥Τσ“ΒΒΡΡ≥÷÷≤ζΤΖ÷–≥ι»Γ![]() ΦΰΘ§≤βΝΩ’β–©≤ζΤΖΒΡ“Μœν÷ ΝΩ÷Η±ξ÷ΒΘ§”…≤βΝΩΫαΙϊΒΟ»γœ¬ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
ΦΰΘ§≤βΝΩ’β–©≤ζΤΖΒΡ“Μœν÷ ΝΩ÷Η±ξ÷ΒΘ§”…≤βΝΩΫαΙϊΒΟ»γœ¬ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
Θ®ΔώΘ©«σ’β![]() Φΰ≤ζΤΖ÷ ΝΩ÷Η±ξ÷ΒΒΡ―υ±ΨΤΫΨυ ΐ
Φΰ≤ζΤΖ÷ ΝΩ÷Η±ξ÷ΒΒΡ―υ±ΨΤΫΨυ ΐ![]() ΚΆ―υ±ΨΖΫ≤ν
ΚΆ―υ±ΨΖΫ≤ν![]() Θ®Ά§“ΜΉι ΐΨί”ΟΗΟ«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μΘ§Φ«Ής
Θ®Ά§“ΜΉι ΐΨί”ΟΗΟ«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μΘ§Φ«Ής![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Θ®ΔρΘ©”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…“‘»œΈΣΘ§’β÷÷≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β![]() Ζΰ¥”’ΐΧ§Ζ÷≤Φ
Ζΰ¥”’ΐΧ§Ζ÷≤Φ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() ΫϋΥΤΈΣ―υ±ΨΤΫΨυ ΐ
ΫϋΥΤΈΣ―υ±ΨΤΫΨυ ΐ![]() Θ§
Θ§![]() ΫϋΥΤΈΣ―υ±ΨΖΫ≤ν
ΫϋΥΤΈΣ―υ±ΨΖΫ≤ν![]() Θ°
Θ°
Θ®iΘ©»τ Ι![]() ΒΡ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷ΒΗΏ”ΎΤσ“Β÷ΤΕ®ΒΡΚœΗώ±ξΉΦΘ§‘ρΚœΗώ±ξΉΦΒΡ÷ ΝΩ÷Η±ξ÷Β¥σ‘ΦΈΣΕύ…ΌΘΩ
ΒΡ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷ΒΗΏ”ΎΤσ“Β÷ΤΕ®ΒΡΚœΗώ±ξΉΦΘ§‘ρΚœΗώ±ξΉΦΒΡ÷ ΝΩ÷Η±ξ÷Β¥σ‘ΦΈΣΕύ…ΌΘΩ
Θ®iiΘ©»τΗΟΤσ“Β”÷…ζ≤ζΝΥ’β÷÷≤ζΤΖ![]() ΦΰΘ§«“ΟΩΦΰ≤ζΤΖœύΜΞΕάΝΔΘ§‘ρ’β
ΦΰΘ§«“ΟΩΦΰ≤ζΤΖœύΜΞΕάΝΔΘ§‘ρ’β![]() Φΰ≤ζΤΖ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ
Φΰ≤ζΤΖ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ![]() ΒΡΦΰ ΐΉν”–Ω…Ρή «Εύ…ΌΘΩ
ΒΡΦΰ ΐΉν”–Ω…Ρή «Εύ…ΌΘΩ
ΗΫΘΚ≤ΈΩΦ ΐΨί”κΙΪ ΫΘΚ![]() Θ§
Θ§![]() ΘΜ»τ
ΘΜ»τ![]() Θ§‘ρΔΌ
Θ§‘ρΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜΔέ
ΘΜΔέ![]() Θ°
Θ°
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©![]() ΘΜ
ΘΜ![]() ΘΜΘ®ΔρΘ©Θ®iΘ©
ΘΜΘ®ΔρΘ©Θ®iΘ©![]() ΘΜΘ®iiΘ©
ΘΜΘ®iiΘ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®ΔώΘ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΙάΦΤΤΫΨυ ΐΒΡΖΫΖ®Ω…÷±Ϋ”«σΒΟ![]() ΘΜάϊ”ΟΖΫ≤νΦΤΥψΙΪ Ϋ
ΘΜάϊ”ΟΖΫ≤νΦΤΥψΙΪ Ϋ![]() Ω…«σΒΟ―υ±ΨΖΫ≤νΘΜΘ®ΔρΘ©Θ®iΘ©ΗυΨί
Ω…«σΒΟ―υ±ΨΖΫ≤νΘΜΘ®ΔρΘ©Θ®iΘ©ΗυΨί![]() ‘≠‘ρΩ…―ι÷Λ≥ω
‘≠‘ρΩ…―ι÷Λ≥ω![]() Θ§«σΒΟ
Θ§«σΒΟ![]() Φ¥ΈΣΫαΙϊΘΜΘ®iiΘ©ΗυΨί
Φ¥ΈΣΫαΙϊΘΜΘ®iiΘ©ΗυΨί![]() ‘≠‘ρΩ…ΒΟΒΫ
‘≠‘ρΩ…ΒΟΒΫ![]() Θ§¥”ΕχΒΟΒΫ’β
Θ§¥”ΕχΒΟΒΫ’β![]() ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ
≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ![]() ΒΡΦΰ ΐ
ΒΡΦΰ ΐ![]() Ζΰ¥””Ύ
Ζΰ¥””Ύ![]() Θ§
Θ§![]() ΘΜΗυΨίΕΰœνΖ÷≤ΦΗ≈¬ ΙΪ ΫΙΙ‘λ≤ΜΒ» Ϋ
ΘΜΗυΨίΕΰœνΖ÷≤ΦΗ≈¬ ΙΪ ΫΙΙ‘λ≤ΜΒ» Ϋ Θ§Ϋβ≤ΜΒ» ΫΩ…«σΒΟ
Θ§Ϋβ≤ΜΒ» ΫΩ…«σΒΟ![]() Θ§¥”ΕχΩ…ΒΟΫαΙϊ.
Θ§¥”ΕχΩ…ΒΟΫαΙϊ.
Θ®ΔώΘ©
![]()
![]()
Θ®ΔρΘ©”…Χβ“β÷ΣΘΚ![]()
Θ®iΘ©![]()
Γύ![]() ±Θ§¬ζΉψΧβ“β
±Θ§¬ζΉψΧβ“β
Φ¥ΚœΗώ±ξΉΦΒΡ÷ ΝΩ÷Η±ξ÷Β‘ΦΈΣΘΚ![]()
Θ®iiΘ©”…![]()
Ω…÷ΣΟΩΦΰ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ![]() ΒΡ ¬ΦΰΗ≈¬ ΈΣ
ΒΡ ¬ΦΰΗ≈¬ ΈΣ![]()
Φ«’β![]() ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ
≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ![]() ΒΡΦΰ ΐΈΣ
ΒΡΦΰ ΐΈΣ![]()
‘ρ![]() Θ§Τδ÷–
Θ§Τδ÷–![]()
![]() «Γ”–
«Γ”–![]() Φΰ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ
Φΰ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ![]() ΒΡ ¬ΦΰΗ≈¬ ΘΚ
ΒΡ ¬ΦΰΗ≈¬ ΘΚ![]()
‘ρ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]()
![]() Β±
Β±![]() ±Θ§
±Θ§![]() ΘΜ
ΘΜ
Β±![]() ±Θ§
±Θ§![]()
”…¥ΥΩ…÷ΣΘ§‘Ύ’β![]() Φΰ≤ζΤΖ÷–Θ§÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ
Φΰ≤ζΤΖ÷–Θ§÷ ΝΩ÷Η±ξ÷Β≤ΜΒΆ”Ύ![]() ΒΡΦΰ ΐΉν”–Ω…Ρή «
ΒΡΦΰ ΐΉν”–Ω…Ρή «![]()


 ”≈―ßΟϊ ΠΟϊΧβœΒΝ–¥πΑΗ
”≈―ßΟϊ ΠΟϊΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
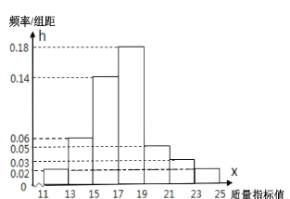
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΒ»―ϋΧί–Έ![]() ÷–Θ§
÷–Θ§![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΒΡ÷–Βψ.œ÷Ζ÷±π―Ί
ΒΡ÷–Βψ.œ÷Ζ÷±π―Ί![]() ΫΪ
ΫΪ![]() ΚΆ
ΚΆ![]() ’έΤπΘ§ ΙΒΟΤΫΟφ
’έΤπΘ§ ΙΒΟΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§ΤΫΟφ
Θ§ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§»γΆΦ2Θ°
Θ§»γΆΦ2Θ°
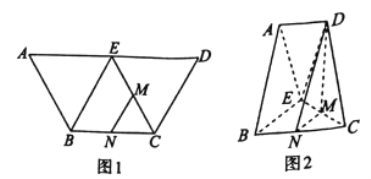
Θ®1Θ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΕύΟφΧε![]() ΒΡΧεΜΐΘ°
ΒΡΧεΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() Θ§Κ· ΐ
Θ§Κ· ΐ![]() ”–ΝΫΗω≤ΜΆ§ΒΡΦΪ÷ΒΒψ
”–ΝΫΗω≤ΜΆ§ΒΡΦΪ÷ΒΒψ![]() Θ§
Θ§![]() Θ°
Θ°
Θ®1Θ©«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©÷ΛΟςΘΚ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2018 Ρξ1‘¬16»’Θ§”…–¬ΜΣΆχΚΆ÷–Ιζ≤ΤΨ≠Νλ–δΝΣΟΥΝΣΚœ÷ςΑλΒΡ2017÷–Ιζ≤ΤΨ≠ΡξΕ»»ΥΈοΤά―ΓΫαΙϊΫ“œΰΘ§Ρ≥÷ΣΟϊΆχ’Ψ≤ΤΨ≠ΤΒΒάΈΣΝΥΫβΙΪ÷ΎΕ‘’β–©ΡξΕ»»ΥΈο «ΖώΝΥΫβΘ§άϊ”ΟΆχ¬γΤΫΧ®Ϋχ––ΝΥΒς≤ιΘ§≤Δ¥”≤Έ”κΒς≤ι’Ώ÷–ΥφΜζ―Γ≥ω![]() »ΥΘ§Α―’β
»ΥΘ§Α―’β![]() »ΥΖ÷ΈΣ
»ΥΖ÷ΈΣ![]() ΝΫάύΘ®
ΝΫάύΘ®![]() άύ±μ ΨΕ‘’β–©ΡξΕ»»ΥΈο±»ΫœΝΥΫβΘ§
άύ±μ ΨΕ‘’β–©ΡξΕ»»ΥΈο±»ΫœΝΥΫβΘ§![]() άύ±μ ΨΕ‘’β–©ΡξΕ»»ΥΈο≤ΜΧΪΝΥΫβΘ©Θ§≤Δ÷Τ≥…»γœ¬±μΗώΘΚ
άύ±μ ΨΕ‘’β–©ΡξΕ»»ΥΈο≤ΜΧΪΝΥΫβΘ©Θ§≤Δ÷Τ≥…»γœ¬±μΗώΘΚ
ΡξΝδΕΈ |
|
|
|
|
»Υ ΐ |
|
|
|
|
|
|
|
|
|
Θ®1Θ©»τΑ¥’’ΡξΝδΕΈΫχ––Ζ÷≤ψ≥ι―υΘ§¥”’β![]() »Υ÷–―Γ≥ω
»Υ÷–―Γ≥ω![]() »ΥΫχ––ΖΟΧΗΘ§≤Δ¥”’β
»ΥΫχ––ΖΟΧΗΘ§≤Δ¥”’β![]() »Υ÷–ΥφΜζ―Γ≥ωΝΫΟϊ–“‘Υ’ΏΗχ”ηΫ±άχ.«σΤδ÷–“ΜΟϊ–“‘Υ’ΏΒΡΡξΝδ‘Ύ
»Υ÷–ΥφΜζ―Γ≥ωΝΫΟϊ–“‘Υ’ΏΗχ”ηΫ±άχ.«σΤδ÷–“ΜΟϊ–“‘Υ’ΏΒΡΡξΝδ‘Ύ![]() ΥξΓΪ
ΥξΓΪ![]() Υξ÷°ΦδΘ§Νμ“ΜΟϊ–“‘Υ’ΏΒΡΡξΝδ‘Ύ
Υξ÷°ΦδΘ§Νμ“ΜΟϊ–“‘Υ’ΏΒΡΡξΝδ‘Ύ![]() ΥξΓΪ
ΥξΓΪ![]() Υξ÷°ΦδΒΡΗ≈¬ ΘΜ(ΉΔΘΚ¥”
Υξ÷°ΦδΒΡΗ≈¬ ΘΜ(ΉΔΘΚ¥”![]() »Υ÷–ΥφΜζ―Γ≥ω
»Υ÷–ΥφΜζ―Γ≥ω![]() »Υ,Ι≤”–
»Υ,Ι≤”–![]() ÷÷≤ΜΆ§―ΓΖ®)
÷÷≤ΜΆ§―ΓΖ®)
Θ®2Θ©»γΙϊΑ―ΡξΝδ‘Ύ![]() ΥξΓΪ
ΥξΓΪ![]() Υξ÷°ΦδΒΡ»Υ≥ΤΈΣ«ύ…ΌΡξΘ§ΡξΝδ‘Ύ
Υξ÷°ΦδΒΡ»Υ≥ΤΈΣ«ύ…ΌΡξΘ§ΡξΝδ‘Ύ![]() ΥξΓΪ
ΥξΓΪ![]() Υξ÷°ΦδΒΡ»Υ≥ΤΈΣ÷–άœΡξΘ§‘ρΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ
Υξ÷°ΦδΒΡ»Υ≥ΤΈΣ÷–άœΡξΘ§‘ρΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣ«ύ…ΌΡξ”κ÷–άœΡξ»Υ‘ΎΕ‘≤ΤΨ≠ΡξΕ»»ΥΈοΒΡΝΥΫβ≥ΧΕ»…œ”–≤ν“λΘΩ
ΒΡ«ΑΧαœ¬»œΈΣ«ύ…ΌΡξ”κ÷–άœΡξ»Υ‘ΎΕ‘≤ΤΨ≠ΡξΕ»»ΥΈοΒΡΝΥΫβ≥ΧΕ»…œ”–≤ν“λΘΩ
≤ΈΩΦ ΐΨίΘΚ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Θ§Τδ÷–
Θ§Τδ÷–![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΐΆ÷‘≤![]() ΒΡΉσΫΙΒψ
ΒΡΉσΫΙΒψ![]() Θ§Ής–±¬ ΈΣ
Θ§Ής–±¬ ΈΣ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() Θ§ΫΜΆ÷‘≤
Θ§ΫΜΆ÷‘≤![]() ”Ύ
”Ύ![]() ΝΫΒψ.
ΝΫΒψ.
Θ®1Θ©»τ‘≠Βψ![]() ΒΫ÷±œΏ
ΒΫ÷±œΏ![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() Θ§«σ÷±œΏ
Θ§«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…ηΒψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΫΜ”ΎΝμ“ΜΒψ
ΫΜ”ΎΝμ“ΜΒψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΫΜ”ΎΝμ“ΜΒψ
ΫΜ”ΎΝμ“ΜΒψ![]() .…η
.…η![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() «ΖώΈΣΕ®÷Β?»τ «Θ§«σ≥ωΗΟΕ®÷ΒΘΜ»τ≤Μ «Θ§«κΥΒΟςάμ”….
«ΖώΈΣΕ®÷Β?»τ «Θ§«σ≥ωΗΟΕ®÷ΒΘΜ»τ≤Μ «Θ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥφΉ≈≥« –ΒΊΧζΫ®…ηΒΡ≥÷–χΆΤΫχΘ§ –ΟώΒΡ≥ω––“≤‘Ϋά¥‘Ϋ±ψάϊΘ°ΗυΨί¥σ ΐΨίΆ≥ΦΤΘ§Ρ≥ΧθΒΊΧζœΏ¬Ζ‘Υ–– ±Θ§ΖΔ≥Β ±ΦδΦδΗτtΘ®ΒΞΈΜΘΚΖ÷÷”Θ©¬ζΉψΘΚ4ΓήtΓή15Θ§![]() NΘ§ΤΫΨυΟΩΧΥΒΊΧζΒΡ‘ΊΩΆ»Υ ΐp(t)Θ®ΒΞΈΜΘΚ»ΥΘ©”κΖΔ≥Β ±ΦδΦδΗτtΫϋΥΤΒΊ¬ζΉψœ¬Ν–Κ· ΐΙΊœΒΘΚ
NΘ§ΤΫΨυΟΩΧΥΒΊΧζΒΡ‘ΊΩΆ»Υ ΐp(t)Θ®ΒΞΈΜΘΚ»ΥΘ©”κΖΔ≥Β ±ΦδΦδΗτtΫϋΥΤΒΊ¬ζΉψœ¬Ν–Κ· ΐΙΊœΒΘΚ Θ§Τδ÷–
Θ§Τδ÷–![]() .
.
(1Θ©»τΤΫΨυΟΩΧΥΒΊΧζΒΡ‘ΊΩΆ»Υ ΐ≤Μ≥§Ιΐ1500»ΥΘ§ ‘«σΖΔ≥Β ±ΦδΦδΗτtΒΡ÷ΒΘ°
(2Θ©»τΤΫΨυΟΩΧΥΒΊΧζΟΩΖ÷÷”ΒΡΨΜ ’“φΈΣ![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©Θ§Έ Β±ΖΔ≥Β ±ΦδΦδΗτtΈΣΕύ…Ό ±Θ§ΤΫΨυΟΩΧΥΒΊΧζΟΩΖ÷÷”ΒΡΨΜ ’“φΉν¥σΘΩΨ°«σ≥ωΉν¥σΨΜ ’“φΘ°
Θ®ΒΞΈΜΘΚ‘ΣΘ©Θ§Έ Β±ΖΔ≥Β ±ΦδΦδΗτtΈΣΕύ…Ό ±Θ§ΤΫΨυΟΩΧΥΒΊΧζΟΩΖ÷÷”ΒΡΨΜ ’“φΉν¥σΘΩΨ°«σ≥ωΉν¥σΨΜ ’“φΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡΫΙΨύΈΣ
ΒΡΫΙΨύΈΣ![]() Θ§Ά÷‘≤
Θ§Ά÷‘≤![]() …œ»Έ“β“ΜΒψΒΫΆ÷‘≤ΝΫΗωΫΙΒψΒΡΨύάκ÷°ΚΆΈΣ6Θ°
…œ»Έ“β“ΜΒψΒΫΆ÷‘≤ΝΫΗωΫΙΒψΒΡΨύάκ÷°ΚΆΈΣ6Θ°
Θ®ΔώΘ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©…η÷±œΏ![]()
![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΘ§Βψ
ΝΫΒψΘ§Βψ![]() Θ®0Θ§1Θ©Θ§«“
Θ®0Θ§1Θ©Θ§«“![]() =
=![]() Θ§«σ÷±œΏ
Θ§«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘ°
ΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©ΘΫΘ®x©¹2Θ©ex©¹![]() +
+![]() xΘ§Τδ÷–
xΘ§Τδ÷–![]() Γ RΘ§e «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ°
Γ RΘ§e «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ°
Θ®1Θ©Β±![]() ΘΨ0 ±Θ§Χ÷¬έΚ· ΐfΘ®xΘ©‘ΎΘ®1Θ§+ΓόΘ©…œΒΡΒΞΒς–‘ΘΜ
ΘΨ0 ±Θ§Χ÷¬έΚ· ΐfΘ®xΘ©‘ΎΘ®1Θ§+ΓόΘ©…œΒΡΒΞΒς–‘ΘΜ
Θ®2Θ©»τΚ· ΐgΘ®xΘ©ΘΫf![]() Θ®xΘ©+2©¹
Θ®xΘ©+2©¹![]() Θ§÷ΛΟςΘΚ ΙgΘ®xΘ©Γί0‘Ύ
Θ§÷ΛΟςΘΚ ΙgΘ®xΘ©Γί0‘Ύ![]() …œΚψ≥…ΝΔΒΡ Β ΐaΡή»ΓΒΫΒΡΉν¥σ’ϊ ΐ÷ΒΈΣ1Θ°
…œΚψ≥…ΝΔΒΡ Β ΐaΡή»ΓΒΫΒΡΉν¥σ’ϊ ΐ÷ΒΈΣ1Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ®“ε‘ΎR…œΒΡΤφΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±,
±, 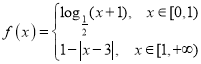
‘ρΚ· ΐ![]() ΒΡΥυ”–ΝψΒψ÷°ΚΆΈΣ_____Θ°
ΒΡΥυ”–ΝψΒψ÷°ΚΆΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com