
����Ŀ��Ϊ����������ߵ�����Ч�ʣ������������ߵ��豸�����˼�������.Ϊ�˶Աȼ���������Ч�����ɼ��������ߵļ�������ǰ���![]() �������������е�ʱ�䳤�ȣ���λ���죩���ݣ����������羥Ҷͼ��
�������������е�ʱ�䳤�ȣ���λ���죩���ݣ����������羥Ҷͼ��
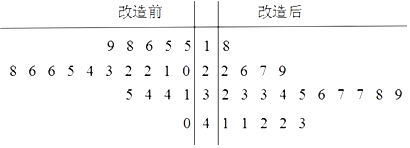
��1���������ɼ���![]() ��������������ʱ�����λ��
��������������ʱ�����λ��![]() ������������������ʱ�䳬��
������������������ʱ�䳬��![]() �Ͳ�����
�Ͳ�����![]() �Ĵ��������������������
�Ĵ��������������������
���� | ������ | |
����ǰ |
|
|
����� |
|
|
�ڸ��ݢ��е����������ܷ���![]() �İ�����Ϊ������������ǰ���������������ʱ���в��죿
�İ�����Ϊ������������ǰ���������������ʱ���в��죿
����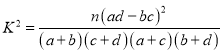 .
.
|
|
|
|
|
|
|
|
��2�������������ߵ�������Ҫ����ά���������������ߵ�����ά�����ð�������ά���ѡ�����ά��������.���������趨ά������Ϊ![]() �죨���ӿ������е���
�죨���ӿ������е���![]() ��
��![]() ����ά��.��������һ���������������ü���ά�����ڣ�ÿ��ά�����������.��һ��ά�������ڣ������������������У����������ά���ѣ��������߲����������У����������ά����.�����㣬����ά����Ϊ
����ά��.��������һ���������������ü���ά�����ڣ�ÿ��ά�����������.��һ��ά�������ڣ������������������У����������ά���ѣ��������߲����������У����������ά����.�����㣬����ά����Ϊ![]() ��Ԫ/�Σ�����ά���ѵ�һ��Ϊ
��Ԫ/�Σ�����ά���ѵ�һ��Ϊ![]() ��Ԫ/���ڣ��˺�ÿ����һ������ά��������
��Ԫ/���ڣ��˺�ÿ����һ������ά��������![]() ��Ԫ.���ƶ�������һ���������ڣ���
��Ԫ.���ƶ�������һ���������ڣ���![]() ��ƣ��ڵ�ά��������
��ƣ��ڵ�ά��������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .���������ڼ��������һ��ά���������������������е�Ƶ����Ϊ���ʣ���һ����������������ά���ѵķֲ��м�����ֵ.
.���������ڼ��������һ��ά���������������������е�Ƶ����Ϊ���ʣ���һ����������������ά���ѵķֲ��м�����ֵ.
���𰸡���1�������������������![]() �İ�����Ϊ������������ǰ���������������ʱ���в��죻��2���𰸲�Ψһ�����������.
�İ�����Ϊ������������ǰ���������������ʱ���в��죻��2���𰸲�Ψһ�����������.
��������
��1�����ɾ�Ҷͼ�е����ݵõ���λ��![]() ���ɴ˿��г�����
���ɴ˿��г�����
�ڸ��ݢ��е�![]() ���������
���������![]() �Ĺ۲�ֵ���ٽ���ٽ�ֵ���жϼ��ɣ�
�Ĺ۲�ֵ���ٽ���ٽ�ֵ���жϼ��ɣ�
��2��![]() ���һ��������������
���һ��������������![]() ��ά�����ڣ�һ��ά������Ϊ
��ά�����ڣ�һ��ά������Ϊ![]() �죬һ��ά�������ڣ����������ڼ��������һ��ά���������������������е�Ƶ����Ϊ���ʣ��ɵ�
�죬һ��ά�������ڣ����������ڼ��������һ��ά���������������������е�Ƶ����Ϊ���ʣ��ɵ�![]() ����һ��������������Ҫ
����һ��������������Ҫ![]() ��ά�����ɵ�
��ά�����ɵ�![]() ����һ�����������ڱ���ά��
����һ�����������ڱ���ά��![]() �ε�����ά����Ϊ
�ε�����ά����Ϊ![]() ��Ԫ����һ�����������ڵ�����ά����Ϊ
��Ԫ����һ�����������ڵ�����ά����Ϊ![]() ��Ԫ���ɵó�
��Ԫ���ɵó�![]() �Ŀ���ȡֵ��д���ֲ��У������ѧ��������.
�Ŀ���ȡֵ��д���ֲ��У������ѧ��������.
��1�����ɾ�Ҷͼ�����ݿɵ���λ��![]() ��
��
���ݾ�Ҷͼ�ɵã�![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ���������±���ʾ��
���������±���ʾ��
���� | ������ | |
����ǰ |
|
|
����� |
|
|
�ڸ��ݢ��е���������![]() ��
��
��ˣ���![]() �İ�����Ϊ������������ǰ���������������ʱ���в��죻
�İ�����Ϊ������������ǰ���������������ʱ���в��죻
��2��![]() ���һ��������������
���һ��������������![]() ��ά�����ڣ�һ��ά������Ϊ
��ά�����ڣ�һ��ά������Ϊ![]() �죬
�죬
һ��ά�������ڣ����������ڼ��������һ��ά���������������������е�Ƶ����Ϊ���ʣ���![]() ��
��
��һ��������������Ҫ![]() ��ά����
��ά����![]() ������ά����Ϊ
������ά����Ϊ![]() ��Ԫ��
��Ԫ��
����ά����Ϊ����Ϊ![]() ������Ϊ
������Ϊ![]() �ĵȲ����У���
�ĵȲ����У���![]() ��ά����Ҫ�ı��Ϸ�Ϊ
��ά����Ҫ�ı��Ϸ�Ϊ![]() ��Ԫ��
��Ԫ��
��һ�����������ڱ���ά��![]() �ε�����ά����Ϊ
�ε�����ά����Ϊ![]() ��Ԫ��
��Ԫ��
��һ�����������ڵ�����ά����Ϊ![]() ��Ԫ����
��Ԫ����![]() ����ȡֵΪ
����ȡֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
|
|
|
|
|
|
|
|
|
��![]() ����Ԫ��.
����Ԫ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ����������Բ
Ϊ����������Բ![]() ����ֱ��
����ֱ��![]() �ԳƵ�ԲΪ
�ԳƵ�ԲΪ![]() ����ԭ��
����ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���ᣬȡ��ͬ�ij��ȵ�λ����������ϵ��ֱ��
���������Ϊ���ᣬȡ��ͬ�ij��ȵ�λ����������ϵ��ֱ��![]() �ļ����귽����
�ļ����귽����![]() ��
��
��1����ֱ��![]() ��
��![]() ���
���![]() ��Ľ���ֱ�Ϊ
��Ľ���ֱ�Ϊ![]() ��
��![]() ��
��![]() ΪԲ
ΪԲ![]() �ϵ�����һ�㣬��
�ϵ�����һ�㣬��![]() �����ֵ��
�����ֵ��
��2������![]() ����ֱ��
����ֱ��![]() ƽ�е�ֱ��
ƽ�е�ֱ��![]() ��Բ
��Բ![]() ��
��![]() ��
��![]() ���㣬��
���㣬��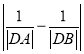 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������������ȱˮ�Ĺ���֮һ������ȱˮ�����Ϊͻ����ij��Ϊ�˽�Լ������ˮ���ƻ��ڱ������о���������ˮ�������(��ȷ��һ�������¾���ˮ��������ˮ��������![]() �IJ��ְ���ƽ���շѣ�����
�IJ��ְ���ƽ���շѣ�����![]() �IJ��ְ�������շ�)��Ϊ�˽�Ϊ������ȷ�����������ͨ�����������40λ����ij����¾���ˮ��(��λ����)�����շ���
�IJ��ְ�������շ�)��Ϊ�˽�Ϊ������ȷ�����������ͨ�����������40λ����ij����¾���ˮ��(��λ����)�����շ���![]() ������Ƶ�ʷֲ�ֱ��ͼ��
������Ƶ�ʷֲ�ֱ��ͼ��
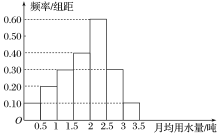
��1����Ƶ�ʷֲ�ֱ��ͼ�й��Ƹ�40λ�����¾���ˮ������������λ����
��2�������������¾���ˮ������1�ֵľ����������ȡ���ˣ����������¾���ˮ����������0.5�ֵĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() (a��b
(a��b![]() R).
R).
��1����b����1ʱ������![]() ��������ֵ����a��ȡֵ��Χ��
��������ֵ����a��ȡֵ��Χ��
��2����a��b��1ʱ������![]() ����СֵΪ2����a��ֵ��
����СֵΪ2����a��ֵ��
��3���������������ʵ��a��b��֤��������ʵ��![]() ����
����![]() ʱ��
ʱ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() .
.
��1����![]() �����.��
�����.��![]() �����ֵ
�����ֵ![]() ��
��
��2����![]() ��ȡ��1���е�
��ȡ��1���е�![]() ����
����![]() ʱ��֤����
ʱ��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ԲPO�У�AB��ԲO��ֱ������AB��4��C�ǵ���ԲO��һ�㣬��AC��2![]() ����DΪ�뾶OB���е㣬����PD.
����DΪ�뾶OB���е㣬����PD.
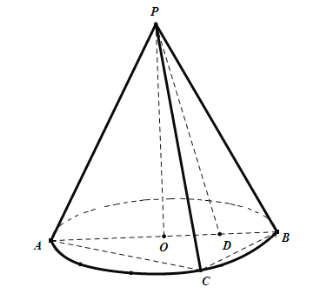
��1����֤��PC��ƽ��APB�ڵ���Ӱ��PD��
��2����PA��4�������Բ��O��ƽ��PBC�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4������![]() ��,
��, ![]() ����
����![]() �ֱ���
�ֱ���![]() ���е㣬
���е㣬 ![]() ����
����![]() ��
��![]() ���۵�
���۵�![]() ������
������![]() ���õ���ͼ������
���õ���ͼ������![]() ����
����![]()
��1����֤�� ![]() ƽ��
ƽ��![]() ��2��������
��2��������![]() ������ֵ.
������ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬��
���е㣬��![]() .
.
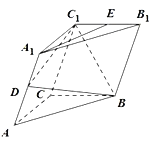
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵ�����ֵ.
���������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() Ϊ������
Ϊ������![]() �Ľ��㣬��
�Ľ��㣬��![]() ��������
��������![]() �ϣ�����
�ϣ�����![]() ��ֱ�߽�������
��ֱ�߽�������![]() ��
��![]() ���㣬�߶�
���㣬�߶�![]() ���е�Ϊ
���е�Ϊ![]() ��������
��������![]() ��
��
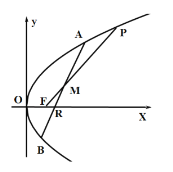
��1����ֱ��![]() ��б��Ϊ1�����
��б��Ϊ1�����![]() �����ꣻ
�����ꣻ
��2����![]() �����ı���
�����ı���![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com