
【题目】在正方体![]() 中,点
中,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,过点
的中点,过点![]() 作平面
作平面![]() 使
使![]() 平面
平面![]() ,
,![]() 平面
平面![]() 若直线
若直线![]() 平面
平面![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
作出图形,设平面![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,推导出
,推导出![]() ,由线面平行的性质定理可得出
,由线面平行的性质定理可得出![]() ,可得出点
,可得出点![]() 为
为![]() 的中点,同理可得出点
的中点,同理可得出点![]() 为
为![]() 的中点,结合中位线的性质可求得
的中点,结合中位线的性质可求得![]() 的值.
的值.
如下图所示:
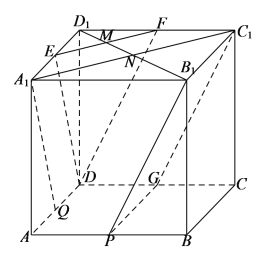
设平面![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,
![]() 四边形
四边形![]() 为正方形,
为正方形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,则
的中点,则![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() 且
且![]() ,
,
![]() 且
且![]() ,
,![]() 且
且![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,![]() 平面
平面![]() ,则存在直线
,则存在直线![]() 平面
平面![]() ,使得
,使得![]() ,
,
若![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,
,
此时,平面![]() 为平面
为平面![]() ,直线
,直线![]() 不可能与平面
不可能与平面![]() 平行,
平行,
所以,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
![]() ,所以,四边形
,所以,四边形![]() 为平行四边形,可得
为平行四边形,可得![]() ,
,
![]() 为
为![]() 的中点,同理可证
的中点,同理可证![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,因此,
,因此,![]() .
.
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,已知抛物线的标准方程为![]() ,其中
,其中![]() 为坐标原点,抛物线的焦点坐标为
为坐标原点,抛物线的焦点坐标为![]() ,
,![]() 为抛物线上任意一点(原点除外),直线
为抛物线上任意一点(原点除外),直线![]() 过焦点
过焦点![]() 交抛物线于
交抛物线于![]() 点,直线
点,直线![]() 过点
过点![]() 交抛物线于
交抛物线于![]() 点,连结
点,连结![]() 并延长交抛物线于
并延长交抛物线于![]() 点.
点.
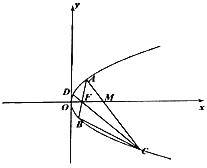
(1)若弦![]() 的长度为8,求
的长度为8,求![]() 的面积;
的面积;
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左右焦点,且椭圆
的左右焦点,且椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过
过![]() 时
时![]() 周长为8.
周长为8.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,是否存在定圆
,是否存在定圆![]() ,使得动直线
,使得动直线![]() 与之相切,若存在写出圆的方程,并求出
与之相切,若存在写出圆的方程,并求出![]() 的面积的取值范围;若不存在,请说明理由.
的面积的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了勾股定理的绝妙证明.如图是赵爽弦图及注文.弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2.若图中勾股形的勾股比为![]() ,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() ,
,![]() )
)
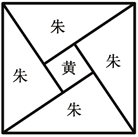
A.2B.4C.6D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情爆发以来,相关疫苗企业发挥专业优势与技术优势争分夺秒开展疫苗研发.为测试疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),选定2000个样本分成三组,测试结果如“下表:
|
|
| |
疫苗有效 | 673 |
|
|
疫苗无效 | 77 | 90 |
|
已知在全体样本中随机抽取1个,抽到![]() 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33.
(1)求![]() ,
,![]() 的值;
的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,求![]() 组应抽取多少个?
组应抽取多少个?
(3)已知![]() ,
,![]() ,求疫苗能通过测试的概率.
,求疫苗能通过测试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍[chúméng]”的五面体(如图),四边形![]() 为矩形,棱
为矩形,棱![]() .若此几何体中,
.若此几何体中,![]() ,
,![]() 和
和![]() 都是边长为
都是边长为![]() 的等边三角形,则此几何体的体积为( )
的等边三角形,则此几何体的体积为( )
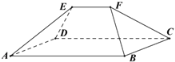
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com