
【题目】对于定义在![]() 上的函数
上的函数![]() ,如果存在两条平行直线
,如果存在两条平行直线![]() 与
与![]()
![]() ,使得对于任意
,使得对于任意![]() ,都有
,都有![]() 恒成立,那么称函数
恒成立,那么称函数![]() 是带状函数,若
是带状函数,若![]() ,
,![]() 之间的最小距离
之间的最小距离![]() 存在,则称
存在,则称![]() 为带宽.
为带宽.
(1)判断函数![]() 是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
是不是带状函数?如果是,指出带宽(不用证明);如果不是,说明理由;
(2)求证:函数![]() (
(![]() )是带状函数;
)是带状函数;
(3)求证:函数![]() (
(![]() )为带状函数的充要条件是
)为带状函数的充要条件是![]() .
.
【答案】(1)是,带宽![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
(1)先理解带状函数的特征,再求函数的值域即可得解;
(2)由函数![]() ,(
,(![]() )的图像表示双曲线
)的图像表示双曲线![]() 在第一象限的部分,
在第一象限的部分,
再结合双曲线的渐近线即可找出两平行直线;
(3)由分段函数的图像特征,结合带状函数的定义,分别证明充分性及必要性即可.
解:(1)因为![]() ,所以
,所以![]() ,
,
取直线![]() ,则
,则![]() 恒成立,
恒成立,
即函数![]() 是带状函数,带宽为
是带状函数,带宽为![]() ;
;
(2)因为![]() ,(
,(![]() )表示双曲线
)表示双曲线![]() 在第一象限的部分,又双曲线的渐近线方程为
在第一象限的部分,又双曲线的渐近线方程为![]() ,故函数
,故函数![]() 满足
满足![]() ,则函数
,则函数![]() 为
为![]() 有一个宽带为
有一个宽带为![]() 的带状函数;
的带状函数;
(3)函数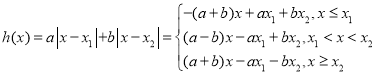 ,
,
先证充分性,当![]() 时,
时,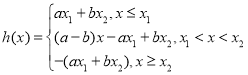 ,
,
不妨设![]() ,则
,则![]() ,即存在直线
,即存在直线![]() ,
,![]() ,满足题意,即函数
,满足题意,即函数![]() 为带状函数,
为带状函数,
再证必要性,当函数![]() (
(![]() )为带状函数,
)为带状函数,
则存在![]() ,又
,又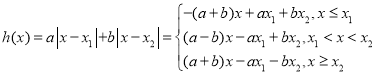 ,当
,当![]() ,则直线
,则直线![]() 与两直线
与两直线![]() ,
,![]() 中至少一条相交,故不满足
中至少一条相交,故不满足![]() ,即
,即![]() 不满足题意,即
不满足题意,即![]() ,
,
故函数![]() (
(![]() )为带状函数的充要条件是
)为带状函数的充要条件是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某旅游胜地欲开发一座景观山,从山的侧面进行勘测,迎面山坡线![]() 由同一平面的两段抛物线组成,其中
由同一平面的两段抛物线组成,其中![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向下,
为顶点、开口向下,![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向上,以过山脚(点
为顶点、开口向上,以过山脚(点![]() )的水平线为
)的水平线为![]() 轴,过山顶(点
轴,过山顶(点![]() )的铅垂线为
)的铅垂线为![]() 轴建立平面直角坐标系如图(单位:百米).已知
轴建立平面直角坐标系如图(单位:百米).已知![]() 所在抛物线的解析式
所在抛物线的解析式![]() ,
,![]() 所在抛物线的解析式为
所在抛物线的解析式为![]()
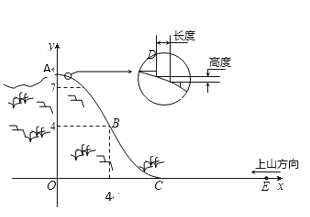
(1)求![]() 值,并写出山坡线
值,并写出山坡线![]() 的函数解析式;
的函数解析式;
(2)在山坡上的700米高度(点![]() )处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点
)处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点![]() 处,
处,![]() (米),假设索道
(米),假设索道![]() 可近似地看成一段以
可近似地看成一段以![]() 为顶点、开口向上的抛物线
为顶点、开口向上的抛物线![]() 当索道在
当索道在![]() 上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
(3)为了便于旅游观景,拟从山顶开始、沿迎面山坡往山下铺设观景台阶,台阶每级的高度为20厘米,长度因坡度的大小而定,但不得少于20厘米,每级台阶的两端点在坡面上(见图).试求出前三级台阶的长度(精确到厘米),并判断这种台阶能否一直铺到山脚,简述理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔![]() 、
、![]() 与桥面
与桥面![]() 垂直,通过测量得知
垂直,通过测量得知![]() ,
,![]() ,当
,当![]() 为
为![]() 中点时,
中点时,![]() .
.
(1)求![]() 的长;
的长;
(2)试问![]() 在线段
在线段![]() 的何处时,
的何处时,![]() 达到最大.
达到最大.

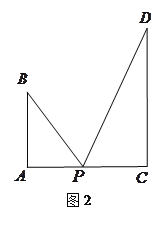
图1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
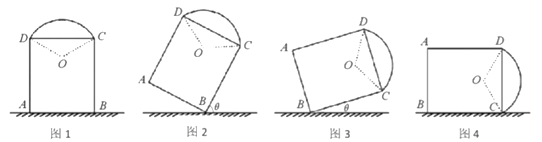
【题目】如图1,一艺术拱门由两部分组成,下部为矩形![]() 的长分别为
的长分别为![]() 米和
米和![]() 米,上部是圆心为
米,上部是圆心为![]() 的劣弧
的劣弧![]() ,
,![]()
(1)求图1中拱门最高点到地面的距离:
(2)现欲以![]() 点为支点将拱门放倒,放倒过程中矩形
点为支点将拱门放倒,放倒过程中矩形![]() 所在的平面始终与地面垂直,如图2、图3、图4所示,设
所在的平面始终与地面垂直,如图2、图3、图4所示,设![]() 与地面水平线
与地面水平线![]() 所成的角为
所成的角为![]() .若拱门上的点到地面的最大距离恰好为
.若拱门上的点到地面的最大距离恰好为![]() 到地面的距离,试求
到地面的距离,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]()
(Ⅰ)若![]() ,请写出
,请写出![]() 的值;
的值;
(Ⅱ)求证:“数列![]() 是等差数列”是“数列
是等差数列”是“数列![]() 是等差数列”的充要条件;
是等差数列”的充要条件;
(Ⅲ)若![]() ,求证:存在
,求证:存在![]() ,使得
,使得![]() ,有
,有![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的正整数![]() ,若数列
,若数列![]() 满足
满足![]() 对任意正整数
对任意正整数![]() 恒成立,则称数列
恒成立,则称数列![]() 是
是![]() 数列,若正数项数列
数列,若正数项数列![]() ,满足:
,满足:![]() 对任意正整数
对任意正整数![]() 恒成立,则称
恒成立,则称![]() 是
是![]() 数列;
数列;
(1)已知正数项数列![]() 是
是![]() 数列,且前五项分别为
数列,且前五项分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为常数,且
为常数,且![]() 是
是![]() 数列,求
数列,求![]() 的最小值;
的最小值;
(3)对于下列两种情形,只要选作一种,满分分别是 ①![]() 分,②
分,②![]() 分,若选择了多于一种情形,则按照序号较小的解答记分.
分,若选择了多于一种情形,则按照序号较小的解答记分.
① 证明:数列![]() 是等差数列的充要条件为“
是等差数列的充要条件为“![]() 既是
既是![]() 数列,又是
数列,又是![]() 数列”;
数列”;
②证明:正数项数列![]() 是等比数列的充要条件为“数列
是等比数列的充要条件为“数列![]() 既是
既是![]() 数列,又是
数列,又是![]() 数列”.
数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 对任意的
对任意的![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为
为![]() 上的“淡泊”函数.
上的“淡泊”函数.
(1)判断![]() 是否为
是否为![]() 上的“淡泊”函数,说明理由;
上的“淡泊”函数,说明理由;
(2)是否存在实数![]() ,使
,使![]() 为
为![]() 上的“淡泊”函数,若存在,求出
上的“淡泊”函数,若存在,求出![]() 的取值范围;不存在,说明理由;
的取值范围;不存在,说明理由;
(3)设![]() 是
是![]() 上的“淡泊”函数(其中
上的“淡泊”函数(其中![]() 不是常值函数),且
不是常值函数),且![]() ,若对任意的
,若对任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com