
ΓΨΧβΡΩΓΩΥφΉ≈»ΥΟώ…ζΜνΥ°ΤΫΒΡΧαΗΏΘ§Ε‘≥« –Ω’Τχ÷ ΝΩΒΡΙΊΉΔΕ»“≤÷π≤Ϋ‘ω¥σΘ§œ¬ΆΦ «Ρ≥≥« –1‘¬÷Ν8‘¬ΒΡΩ’Τχ÷ ΝΩΦλ≤β«ιΩωΘ§ΆΦ÷–“ΜΓΔΕΰΓΔ»ΐΓΔΥΡΦΕ «Ω’Τχ÷ ΝΩΒ»ΦΕΘ§“ΜΦΕΩ’Τχ÷ ΝΩΉνΚΟΘ§“ΜΦΕΚΆΕΰΦΕΕΦ «÷ ΝΩΚœΗώΧλΤχΘ§œ¬ΟφΥΡ÷÷ΥΒΖ®’ΐ»ΖΒΡ «Θ® Θ©
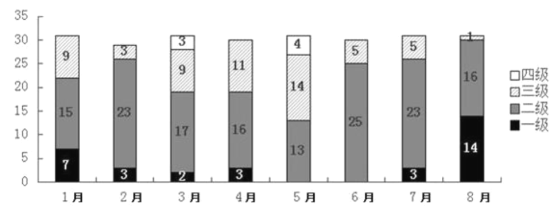
ΔΌ1‘¬÷Ν8‘¬Ω’ΤχΚœΗώΧλ ΐ≥§Ιΐ24ΧλΒΡ‘¬Ζί”–3Ηω
ΔΎΒΎΕΰΦΨΕ»”κΒΎ“ΜΦΨΕ»œύ±»Θ§Ω’ΤχΚœΗώΧλ ΐΒΡ±»÷Ίœ¬ΫΒΝΥ
Δέ8‘¬ «Ω’Τχ÷ ΝΩΉνΚΟΒΡ“ΜΗω‘¬
Δή6‘¬ΒΡΩ’Τχ÷ ΝΩΉν≤ν
A.ΔΎΔέB.ΔΌΔΎΔέC.ΔΌΔέΔήD.ΔΎΔέΔή
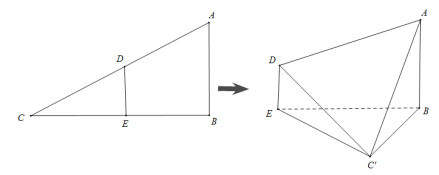
ΓΨ¥πΑΗΓΩA
ΓΨΫβΈωΓΩ
‘ΎΔΌ÷–,1‘¬÷Ν8‘¬Ω’ΤχΚœΗώΧλ ΐ≥§Ιΐ24ΧλΒΡ‘¬Ζί”–:2‘¬,6‘¬,7‘¬,8‘¬,Ι≤4Ηω;‘ΎΔΎ÷–,Ζ÷±π«σ≥ωΒΎ“ΜΦΨΕ»ΚœΗώΧλ ΐΒΡ±»÷ΊΚΆΒΎΕΰΦΨΕ»ΚœΗώΧλΤχΒΡ±»÷Ί,Ρή«σ≥ωΫαΙϊ;‘ΎΔέ÷–,8‘¬Ω’Τχ÷ ΝΩΚœΗώΒΡΧλΤχ¥οΒΫ30Χλ;‘ΎΔή÷–,5‘¬Ω’Τχ÷ ΝΩΚœΗώΧλΤχ÷Μ”–13Χλ.
‘ΎΔΌ÷–Θ§1‘¬÷Ν8‘¬Ω’ΤχΚœΗώΧλ ΐ≥§Ιΐ24ΧλΒΡ‘¬Ζί”–ΘΚ 2‘¬Θ§6‘¬Θ§7‘¬Θ§8‘¬Θ§Ι≤4ΗωΘ§Ι ΔΌ≤Μ’ΐ»ΖΘΜ
‘ΎΔΎ÷–Θ§ΒΎ“ΜΦΨΕ»ΚœΗώΧλ ΐΒΡ±»÷ΊΈΣ![]() ΘΜΒΎΕΰΦΨΕ»ΚœΗώΧλΤχΒΡ±»÷ΊΈΣ
ΘΜΒΎΕΰΦΨΕ»ΚœΗώΧλΤχΒΡ±»÷ΊΈΣ![]() Θ§Υυ“‘ΒΎΕΰΦΨΕ»”κΒΎ“ΜΦΨΕ»œύ±»Θ§Ω’Τχ¥ο±ξΧλ ΐΒΡ±»÷Ίœ¬ΫΒΝΥΘ§Υυ“‘ΔΎ «’ΐ»ΖΒΡΘΜ
Θ§Υυ“‘ΒΎΕΰΦΨΕ»”κΒΎ“ΜΦΨΕ»œύ±»Θ§Ω’Τχ¥ο±ξΧλ ΐΒΡ±»÷Ίœ¬ΫΒΝΥΘ§Υυ“‘ΔΎ «’ΐ»ΖΒΡΘΜ
‘ΎΔέ÷–Θ§8‘¬Ω’Τχ÷ ΝΩΚœΗώΧλΤχ¥οΒΫ30ΧλΘ§ «Ω’Τχ÷ ΝΩΉνΚΟΒΡ“ΜΗω‘¬Θ§Υυ“‘Δέ «’ΐ»ΖΒΡΘΜ
‘ΎΔή÷–Θ§5‘¬Ω’Τχ÷ ΝΩΚœΗώΧλΤχ÷Μ”–13ΧλΘ§5‘¬ΖίΒΡΩ’Τχ÷ ΝΩΉν≤νΘ§Υυ“‘Δή «¥μΈσΒΡΘ§
Ήέ…œΩ…÷ΣΘ§’ΐ»ΖΒΡΥΒΖ® «ΔΎΔέΘ§
Ι ―ΓΘΚA.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() ΈΣ≈ΉΈοœΏ
ΈΣ≈ΉΈοœΏ![]() ΒΡΫΙΒψΘ§Ιΐ
ΒΡΫΙΒψΘ§Ιΐ![]() ΒΡΕ·÷±œΏΫΜ≈ΉΈοœΏ
ΒΡΕ·÷±œΏΫΜ≈ΉΈοœΏ![]() ”Ύ
”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ°Β±÷±œΏ”κ
ΝΫΒψΘ°Β±÷±œΏ”κ![]() ÷α¥Ι÷± ±Θ§
÷α¥Ι÷± ±Θ§![]() Θ°
Θ°
Θ®1Θ©«σ≈ΉΈοœΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η÷±œΏ![]() ΒΡ–±¬ ΈΣ1«“”κ≈ΉΈοœΏΒΡΉΦœΏ
ΒΡ–±¬ ΈΣ1«“”κ≈ΉΈοœΏΒΡΉΦœΏ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() Θ§≈ΉΈοœΏ
Θ§≈ΉΈοœΏ![]() …œ¥φ‘ΎΒψ
…œ¥φ‘ΎΒψ![]() ΙΒΟ÷±œΏ
ΙΒΟ÷±œΏ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡ–±¬ ≥…Β»≤ν ΐΝ–Θ§«σΒψ
ΒΡ–±¬ ≥…Β»≤ν ΐΝ–Θ§«σΒψ![]() ΒΡΉχ±ξΘ°
ΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
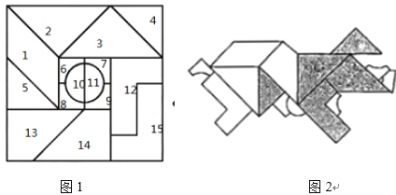
ΓΨΧβΡΩΓΩ °Έε«…ΑεΓΔ”÷≥Τ“φ÷«ΆΦΘ§ΈΣ«ε≥·’ψΫ≠ ΓΒ¬«ε÷ΣœΊΆ·“ΕΗΐ‘ΎΆ§÷ΈΡξΦδΥυΖΔΟςΘ§ΥϋΡήΤ¥≥ω≤ίΡΨΓΔΜ®ΙϊΓΔΡώ όΓΔ”ψ≥φΓΔΈΡΉ÷Β»ΆΦΑΗ. °Έε«…Αε”… °ΈεΩιΑεΉι≥…“ΜΗω¥σ’ΐΖΫ–ΈΘ®»γΆΦ1Θ©Θ§Τδ÷–±ξΚ≈ΈΣ2Θ§3Θ§4Θ§5ΒΡ–ΓΑεΨυΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΆΦ2 «”Ο °Έε«…ΑεΤ¥≥ωΒΡ2019Ρξ…ζ–Λ÷μΒΡΆΦΑΗΘ§‘ρ¥”…ζ–Λ÷μΆΦΑΗ÷–»Έ»Γ“ΜΒψΘ§ΗΟΒψ«ΓΚϻù‘“θ”Α≤ΩΖ÷÷–ΒΡΗ≈¬ ΈΣ______.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©ΘΫ2|x+2|+|x©¹3|Θ°
Θ®1Θ©«σ≤ΜΒ» ΫfΘ®xΘ©Γί8ΒΡΫβΦ·ΘΜ
Θ®2Θ©»τaΘΨ0Θ§bΘΨ0Θ§«“Κ· ΐFΘ®xΘ©ΘΫfΘ®xΘ©©¹3a©¹2b”–Έ®“ΜΝψΒψx0Θ§÷ΛΟςΘΚ![]() fΘ®x0Θ©Θ°
fΘ®x0Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΆ÷‘≤![]() ΙΐΒψ
ΙΐΒψ![]() Θ§άκ–Ρ¬ ΈΣ
Θ§άκ–Ρ¬ ΈΣ![]() Θ§
Θ§![]() Ζ÷±π «Ά÷‘≤
Ζ÷±π «Ά÷‘≤![]() ΒΡΉσΓΔ”“ΕΞΒψΘ§Ιΐ”“ΫΙΒψ
ΒΡΉσΓΔ”“ΕΞΒψΘ§Ιΐ”“ΫΙΒψ![]() «“–±¬ ΈΣ
«“–±¬ ΈΣ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() ΝΫΒψΘ°
ΝΫΒψΘ°
Θ®1Θ©«σΆ÷‘≤![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®2Θ©Φ«![]() ΓΔ
ΓΔ![]() ΒΡΟφΜΐΖ÷±πΈΣ
ΒΡΟφΜΐΖ÷±πΈΣ![]() ΓΔ
ΓΔ![]() Θ§»τ
Θ§»τ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©Φ«÷±œΏ![]() ΓΔ
ΓΔ![]() ΒΡ–±¬ Ζ÷±πΈΣ
ΒΡ–±¬ Ζ÷±πΈΣ![]() ΓΔ
ΓΔ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥Χ «
ΒΡ≤Έ ΐΖΫ≥Χ «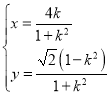 Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©Θ§“‘Ήχ±ξ‘≠Βψ
ΈΣ≤Έ ΐΘ©Θ§“‘Ήχ±ξ‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§![]() ÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§÷±œΏ
÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§÷±œΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() .
.
Θ®1Θ©«ζœΏ![]() ΒΡΤ’Ά®ΖΫ≥ΧΚΆ÷±œΏ
ΒΡΤ’Ά®ΖΫ≥ΧΚΆ÷±œΏ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©«σ«ζœΏ![]() …œΒΡΒψΒΫ÷±œΏ
…œΒΡΒψΒΫ÷±œΏ![]() ΒΡΨύάκΒΡ»Γ÷ΒΖΕΈß.
ΒΡΨύάκΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2019ΡξΒΉΘ§Κΰ±± ΓΈδΚΚ –Β»ΕύΗωΒΊ«χ¬Ϋ–χ≥ωœ÷Η–»Ψ–¬–ΆΙΎΉ¥≤ΓΕΨΖΈ―ΉΒΡΜΦ’Ώ.ΈΣΦΑ ±”––ßΒΊΕ‘“Ώ«ι ΐΨίΫχ––Νς––≤Γ―ßΆ≥ΦΤΖ÷ΈωΘ§Ρ≥ΒΊ―–ΨΩΜζΙΙ’κΕ‘ΗΟΒΊ ΒΦ «ιΩωΘ§ΗυΨίΗΟΒΊΜΦ’Ώ «Ζώ”–ΈδΚΚ¬Ο–– Ζ”κ «Ζώ”–»Ζ’ο≤ΓάΐΫ”¥Ξ ΖΘ§ΫΪ–¬ΙΎΖΈ―ΉΜΦ’ΏΖ÷ΈΣΥΡάύΘΚ”–ΈδΚΚ¬Ο–– ΖΘ®ΈόΫ”¥Ξ ΖΘ©Θ§ΈόΈδΚΚ¬Ο–– ΖΘ®ΈόΫ”¥Ξ ΖΘ©Θ§”–ΈδΚΚ¬Ο–– ΖΘ®”–Ϋ”¥Ξ ΖΘ©ΚΆΈόΈδΚΚ¬Ο–– ΖΘ®”–Ϋ”¥Ξ ΖΘ©Θ§Ά≥ΦΤΒΟΒΫ“‘œ¬œύΙΊ ΐΨί.
Θ®1Θ©«κΫΪΝ–ΝΣ±μΧν–¥Άξ’ϊΘΚ
”–Ϋ”¥Ξ Ζ | ΈόΫ”¥Ξ Ζ | ΉήΦΤ | |
”–ΈδΚΚ¬Ο–– Ζ | 27 | ||
ΈόΈδΚΚ¬Ο–– Ζ | 18 | ||
ΉήΦΤ | 27 | 54 |
Θ®2Θ©ΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.025ΒΡ«ΑΧαœ¬»œΈΣ”–ΈδΚΚ¬Ο–– Ζ”κ”–»Ζ’ο≤ΓάΐΫ”¥Ξ Ζ”–ΙΊœΒΘΩ
ΗΫΘΚ![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ζ÷±π «
Ζ÷±π «![]() ΒΡ÷–ΒψΘ°ΫΪ
ΒΡ÷–ΒψΘ°ΫΪ![]() ―Ί
―Ί![]() ’έ≥…¥σ–Γ «
’έ≥…¥σ–Γ «![]() ΒΡΕΰΟφΫ«
ΒΡΕΰΟφΫ«![]() Θ°
Θ°
Θ®ΔώΘ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©«σ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ßΗΏ»ΐΡξΦΕ‘ΎΖΒ–ΘΗ¥―ßΚσΘ§ΈΣΝΥΉωΚΟ“Ώ«ιΖάΜΛΙΛΉςΘ§“ΜΈΜΖά“ΏΕΫ≤λ‘±“ΣΫΪ2Κ–Άξ»ΪœύΆ§ΒΡ![]() ΩΎ’÷ΚΆ3Κ–Άξ»ΪœύΆ§ΒΡΤ’Ά®“Ϋ”ΟΩΎ’÷»Ϊ≤ΩΖ÷≈δΗχ3Ηω≤ΜΆ§ΒΡΑύΘ§ΟΩΗωΑύ÷Ν…ΌΖ÷ΒΟ“ΜΚ–Θ§‘ρ≤ΜΆ§ΒΡΖ÷Ζ®÷÷ ΐ «Θ® Θ©
ΩΎ’÷ΚΆ3Κ–Άξ»ΪœύΆ§ΒΡΤ’Ά®“Ϋ”ΟΩΎ’÷»Ϊ≤ΩΖ÷≈δΗχ3Ηω≤ΜΆ§ΒΡΑύΘ§ΟΩΗωΑύ÷Ν…ΌΖ÷ΒΟ“ΜΚ–Θ§‘ρ≤ΜΆ§ΒΡΖ÷Ζ®÷÷ ΐ «Θ® Θ©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com