
【题目】已知函数![]() .
.
(1)讨论函数f(x)的极值点的个数;
(2)若f(x)有两个极值点![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)求得函数的导数![]() ,
,![]() ,按
,按![]() 、
、![]() 、
、![]() 三种情况分类讨论,得出函数的单调性,进而得出函数的极值;
三种情况分类讨论,得出函数的单调性,进而得出函数的极值;
(2)由(1)知,当![]() 时,
时,![]() 极值点
极值点![]() ,
,![]() 是方程
是方程![]() 的两根,化简得
的两根,化简得![]() ,设
,设![]() ,
,![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与最值,即可求解.
的单调性与最值,即可求解.
(1)由题意,函数![]() ,
,
得![]() ,
,![]() ,
,
(i)若![]() 时;
时;![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
所以当![]() ,函数
,函数![]() 取得极小值,
取得极小值,![]() 是
是![]() 的一个极小值点;
的一个极小值点;
(ii)若![]() 时,则
时,则![]() ,即
,即![]() 时,此时
时,此时![]() ,
,![]() 在
在![]() 是减函数,
是减函数,![]() 无极值点,
无极值点,
当![]() 时,则
时,则![]() ,令
,令![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 和
和![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 取得极小值,在
取得极小值,在![]() 取得极大值,所以
取得极大值,所以![]() 有两个极值点,
有两个极值点,
综上可知:(i)![]() 时,
时,![]() 仅有一个极值点;(ii).当
仅有一个极值点;(ii).当![]() 时,
时,![]() 无极值点;
无极值点;
(iii)当![]() ,
,![]() 有两个极值点.
有两个极值点.
(2)由(1)知,当且仅当![]() 时,
时,![]() 有极小值点
有极小值点![]() 和极大值点
和极大值点![]() ,
,
且![]() ,
,![]() 是方程
是方程![]() 的两根,∴
的两根,∴![]() ,
,![]() ,
,
则![]()
![]()
![]()
![]()
![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
∴![]() 时,
时,![]() 是减函数,
是减函数,![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
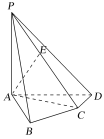
(1)求证:AE⊥平面PCD;
(2)求PB和平面PAD所成的角的大小;
(3)求二面角A-PD-C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂共有![]() 名工人,已知这
名工人,已知这![]() 名工人去年完成的产品数都在区间
名工人去年完成的产品数都在区间![]() (单位:万件)内,其中每年完成
(单位:万件)内,其中每年完成![]() 万件及以上的工人为优秀员工,现将其分成
万件及以上的工人为优秀员工,现将其分成![]() 组,第
组,第![]() 组、第
组、第![]() 组、第
组、第![]() 组、第
组、第![]() 组、第
组、第![]() 组对应的区间分别为
组对应的区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并绘制出如图所示的频率分布直方图.
,并绘制出如图所示的频率分布直方图.
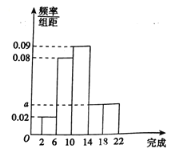
(1)求![]() 的值,并求去年优秀员工人数;
的值,并求去年优秀员工人数;
(2)选取合适的抽样方法从这![]() 名工人中抽取容量为
名工人中抽取容量为![]() 的样本,求这
的样本,求这![]() 组分别应抽取的人数;
组分别应抽取的人数;
(3)现从(2)中![]() 人的样本中的优秀员工中随机选取
人的样本中的优秀员工中随机选取![]() 名传授经验,求选取的
名传授经验,求选取的![]() 名工人在同一组的概率.
名工人在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在五边形AEBCD中,![]() ,C
,C![]() ,
,![]() ,
,![]() ,
,![]() (如图).将△ABE沿AB折起,使平面ABE⊥平面ABCD,线段AB的中点为O(如图).
(如图).将△ABE沿AB折起,使平面ABE⊥平面ABCD,线段AB的中点为O(如图).
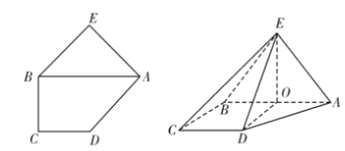
(1)求证:平面ABE⊥平面DOE;
(2)求平面EAB与平面ECD所成的锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年4月1日,新华通讯社发布:国务院决定设立河北雄安新区.消息一出,河北省雄县、容城、安新3县及周边部分区域迅速成为海内外高度关注的焦点.
(1)为了响应国家号召,北京市某高校立即在所属的8个学院的教职员工中作了“是否愿意将学校整体搬迁至雄安新区”的问卷调查,8个学院的调查人数及统计数据如下:
调查人数( | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
愿意整体搬迁人数( | 8 | 17 | 25 | 31 | 39 | 47 | 55 | 66 |
请根据上表提供的数据,用最小二乘法求出变量![]() 关于变量
关于变量![]() 的线性回归方程
的线性回归方程![]() 保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;
保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;
(2)若该校的8位院长中有5位院长愿意将学校整体搬迁至雄安新区,现该校拟在这8位院长中随机选取4位院长组成考察团赴雄安新区进行实地考察,记![]() 为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求
为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式及数据:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 上任意一点,点
上任意一点,点![]() ,线段
,线段![]() 的中垂线交
的中垂线交![]() 于点
于点![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)若动直线![]() 与圆
与圆![]() 相切,且与动点
相切,且与动点![]() 的轨迹交于点
的轨迹交于点![]() 、
、![]() ,求
,求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次调查中,甲、乙、丙、丁四位同学阅读量有如下关系:同学甲、丙阅读量之和与乙、丁阅读量之和相同,同学甲、乙阅读量之和大于丙、丁阅读量之和,丁的阅读量大于乙、丙阅读量之和.那么这四名同学按阅读量从大到小的排序依次为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com