
【题目】已知F为抛物线![]() 的焦点,过点F的直线交抛物线于A,B两点,其中A在x轴上方,O是坐标原点,若
的焦点,过点F的直线交抛物线于A,B两点,其中A在x轴上方,O是坐标原点,若![]() ,
,![]() ,则以AB为直径的圆的标准方程为____.
,则以AB为直径的圆的标准方程为____.
【答案】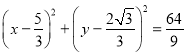
【解析】
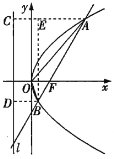
解法一:如图,过点![]() ,
,![]() 分别作抛物线的准线
分别作抛物线的准线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,由抛物线的定义算出
,由抛物线的定义算出![]() ,
,![]() ,则可推出
,则可推出
![]() ,又
,又![]() ,得
,得![]() ,从而确定抛物线的解析式及直线
,从而确定抛物线的解析式及直线![]() 的解析式,最后联立直线
的解析式,最后联立直线![]() 与抛物线的方程,由根与系数关系及弦长公式求得所求圆的圆心和半径,进而求出圆的方程;
与抛物线的方程,由根与系数关系及弦长公式求得所求圆的圆心和半径,进而求出圆的方程;
解法二:如图,过点![]() 分别作抛物线的准线
分别作抛物线的准线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,由抛物线的定义算出
,由抛物线的定义算出![]() ,
,![]() ,则
,则![]() ,求出直线
,求出直线![]() 的斜率,然后借助点到直线的距离公式及三角形面积公式求得
的斜率,然后借助点到直线的距离公式及三角形面积公式求得![]() 的值,从而确定抛物线的解析式及直线
的值,从而确定抛物线的解析式及直线![]() 的解析式,最后联立直线
的解析式,最后联立直线![]() 与抛物线的方程,求得所求圆的圆心和半径,进而求出圆的方程.
与抛物线的方程,求得所求圆的圆心和半径,进而求出圆的方程.
解法一:
如图,过点![]() ,
,![]() 分别作抛物线的准线
分别作抛物线的准线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,∴由抛物线的定义可得
,∴由抛物线的定义可得![]() ,
,
∴![]() ,
,
∵![]() ,
,
又![]() ,
,
∴![]() ,得
,得![]() 易知
易知![]() ,
,
∴直线![]() 的倾斜角为60°,∴直线
的倾斜角为60°,∴直线![]() 的方程为
的方程为![]() ,代入抛物线的方程
,代入抛物线的方程![]() ,得
,得![]() .设
.设![]() ,
,![]() ,则
,则![]() ,
,
∴以![]() 为直径的圆的标准方程为
为直径的圆的标准方程为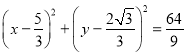 .
.

解法二:
如图,过点![]() 分别作抛物线的准线
分别作抛物线的准线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,∴由抛物线的定义可得
,∴由抛物线的定义可得![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∴直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
∵原点![]() 到直线
到直线![]() 的距离
的距离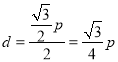 ,且
,且![]() ,
,
∴![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,代入抛物线的方程
,代入抛物线的方程![]() ,
,
得![]() ,
,
设![]() ,则
,则![]() ,
,
∴以![]() 为直径的圆的标准方程为
为直径的圆的标准方程为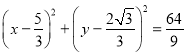 .
.
故答案为: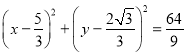


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=2,DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
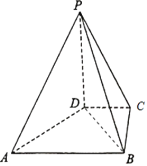
(1)求证:AD⊥PB;
(2)求A点到平面BPC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,__________.在①
,__________.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
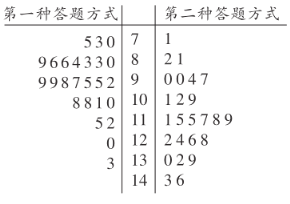
【题目】某市实验中学数学教研组,在高三理科一班进行了一次“采用两种不同方式进行答卷”的考试实验,第一种做卷方式:按从前往后的顺序依次做;第二种做卷方式:先做简单题,再做难题.为了比较这两种做卷方式的效率,选取了![]() 名学生,将他们随机分成两组,每组
名学生,将他们随机分成两组,每组![]() 人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
![]() 若
若![]() 分(含
分(含![]() 分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
![]() 设
设![]() 名学生考试分数的中位数为
名学生考试分数的中位数为![]() ,根据茎叶图填写下面的
,根据茎叶图填写下面的![]() 列联表:
列联表:
超过中位数 | 不超过中位数 | 合计 | |
第一种做卷方式 | |||
第一种做卷方式 | |||
合计 |
根据列联表,能否有![]() 的把握认为两种做卷方式的效率有差异?
的把握认为两种做卷方式的效率有差异?
附: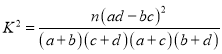 ,
,![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
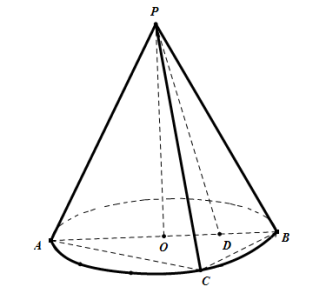
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正△ABC边长为3,点M,N分别是AB,AC边上的点,AN=BM=1,如图1所示.将△AMN沿MN折起到△PMN的位置,使线段PC长为![]() ,连接PB,如图2所示.
,连接PB,如图2所示.
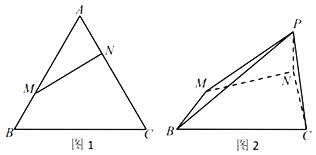
(Ⅰ)求证:平面PMN⊥平面BCNM;
(Ⅱ)若点D在线段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com