
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高
吨,且每吨原材料创造的利润提高![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元
万元![]() .
.
(1)若设备升级后生产这批![]() 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批![]() 产品的利润,求
产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批![]() 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批![]() 产品的利润,求
产品的利润,求![]() 的最大值.
的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ,
,![]() 为常数,
为常数, ![]() .
.
(1)求![]() 的值;(2)若
的值;(2)若![]() 在
在![]() 上为单调函数,求
上为单调函数,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若在
,若在![]() 上至少存在一个
上至少存在一个![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() ).
).
(1)证明:直线![]() 过定点;
过定点;
(2)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,△
,△![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的最小值,并求此时直线
的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
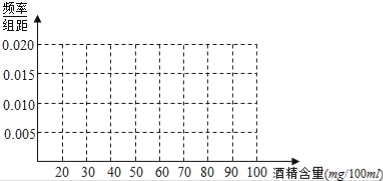
【题目】《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如表:
酒精含量(mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70)[] | [70,80) | [80,90) | [90,100] |
人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(Ⅰ)绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);
(Ⅱ)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的众数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
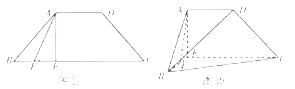
【题目】如图①所示,四边形![]() 为等腰梯形,
为等腰梯形,![]() ,且
,且![]() 于点
于点![]() 为
为![]() 的中点.将
的中点.将![]() 沿着
沿着![]() 折起至
折起至![]() 的位置,得到如图②所示的四棱锥
的位置,得到如图②所示的四棱锥![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com