
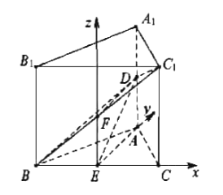
【题目】如图,在直三棱柱ABC﹣A1B1C1中,△ABC是边长为6的等边三角形,D,E分别为AA1,BC的中点.
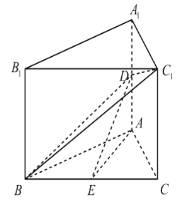
(1)证明:AE//平面BDC1;
(2)若异面直线BC1与AC所成角的余弦值为![]() .求DE与平面BDC1所成角的正弦值.
.求DE与平面BDC1所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先证明四边形ADFE为平行四边形,则AE∥DF,由此即可得证;
(2)以点E为坐标原点,建立空间直角坐标系,设AA1=2t(t>0),根据已知条件可求得![]() ,进而求得平面BDC1的法向量以及直线DE的方向向量,再利用向量公式求解.
,进而求得平面BDC1的法向量以及直线DE的方向向量,再利用向量公式求解.
(1)证明:取BC1的中点F,连接DF,EF,
∵E为BC中点,
∴![]() ∥
∥![]() ,
,![]()
又∵D为AA1的中点,
![]() ∥
∥![]() ,
,![]() ,
,
∴![]() ∥
∥![]() ,
,![]()
![]()
∴四边形ADFE为平行四边形,
∴AE∥DF,
∵AE![]() 平面BDC1,DF
平面BDC1,DF![]() 平面BDC1,
平面BDC1,
∴AE∥平面BDC1;
(2)由(1)及题设可知,BC,EA,EF两两互相垂直,则以点E为坐标原点,EC,EA,
EF所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
设AA1=2t(t>0),则![]() ,
,
所以![]() ,
,
故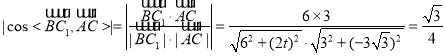
解得![]() ,
,
设平面BDC1的法向量为![]()
由 ,得
,得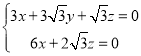 ,
,
令![]() ,则
,则![]() ,
,
又![]() ,
,
所以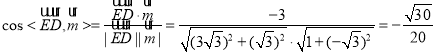 ,
,
设DE与平面BDC1所成角为![]() ,
,
则![]()
![]() ,
,
∴DE与平面BDC1所成角的正弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
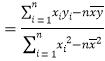 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()

(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,且经过点
的长轴长为4,且经过点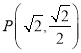 .
.
(1)求椭圆的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,且与椭圆相交于
,且与椭圆相交于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),过
),过![]() 作
作![]() 的角平分线交椭圆于另一点
的角平分线交椭圆于另一点![]() .
.
(i)证明:直线![]() 与坐标轴平行;
与坐标轴平行;
(ii)当![]() 时,求四边形
时,求四边形![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
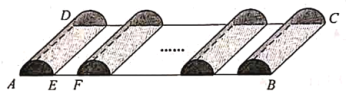
【题目】如图,某人承包了一块矩形土地![]() 用来种植草莓,其中
用来种植草莓,其中![]() m,
m,![]() m.现规划建造如图所示的半圆柱型塑料薄膜大棚
m.现规划建造如图所示的半圆柱型塑料薄膜大棚![]() 个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米
个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米![]() 元;另外,还需在每个大棚之间留下
元;另外,还需在每个大棚之间留下![]() m宽的空地用于建造排水沟与行走小路(如图中
m宽的空地用于建造排水沟与行走小路(如图中![]() m),这部分建设造价为每平方米
m),这部分建设造价为每平方米![]() 元.
元.
(1)当![]() 时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留
时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留![]() )
)
(2)试确定大棚的个数,使得上述两项费用的和最低?(本小题计算中![]() 取
取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面的问题中,并解决该问题.
这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com