
【题目】设函数![]() ,曲线
,曲线![]() 在点(
在点(![]() ,f(
,f(![]() ))处的切线与y轴垂直.
))处的切线与y轴垂直.
(1)求b.
(2)若![]() 有一个绝对值不大于1的零点,证明:
有一个绝对值不大于1的零点,证明:![]() 所有零点的绝对值都不大于1.
所有零点的绝对值都不大于1.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)利用导数的几何意义得到![]() ,解方程即可;
,解方程即可;
(2)由(1)可得![]() ,易知
,易知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增,且
上单调递增,且![]() ,采用反证法,推出矛盾即可.
,采用反证法,推出矛盾即可.
(1)因为![]() ,
,
由题意,![]() ,即
,即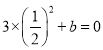
则![]() ;
;
(2)由(1)可得![]() ,
,
![]() ,
,
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增,
上单调递增,
且![]() ,
,
若![]() 所有零点中存在一个绝对值大于1的零点
所有零点中存在一个绝对值大于1的零点![]() ,则
,则![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
当![]() 时,
时,![]() ,
,
又![]() ,
,
由零点存在性定理知![]() 在
在![]() 上存在唯一一个零点
上存在唯一一个零点![]() ,
,
即![]() 在
在![]() 上存在唯一一个零点,在
上存在唯一一个零点,在![]() 上不存在零点,
上不存在零点,
此时![]() 不存在绝对值不大于1的零点,与题设矛盾;
不存在绝对值不大于1的零点,与题设矛盾;
当![]() 时,
时,![]() ,
,
又![]() ,
,
由零点存在性定理知![]() 在
在![]() 上存在唯一一个零点
上存在唯一一个零点![]() ,
,
即![]() 在
在![]() 上存在唯一一个零点,在
上存在唯一一个零点,在![]() 上不存在零点,
上不存在零点,
此时![]() 不存在绝对值不大于1的零点,与题设矛盾;
不存在绝对值不大于1的零点,与题设矛盾;
综上,![]() 所有零点的绝对值都不大于1.
所有零点的绝对值都不大于1.
【点晴】
本题主要考查利用导数研究函数的零点,涉及到导数的几何意义,反证法,考查学生逻辑推理能力,是一道有一定难度的题.


科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC–A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.
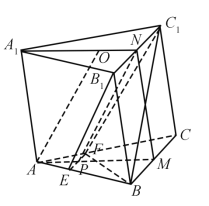
(1)证明:AA1//MN,且平面A1AMN⊥平面EB1C1F;
(2)设O为△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=![]() ,求四棱锥B–EB1C1F的体积.
,求四棱锥B–EB1C1F的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() 且椭圆的短轴长为
且椭圆的短轴长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知动直线![]() 过右焦点
过右焦点![]() ,且与椭圆
,且与椭圆![]() 分别交于
分别交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得,
,使得,![]() 恒成立?若存在求出点
恒成立?若存在求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专项规定.某小区采取一系列措施,宣传垃圾分类的知识与意义,并采购分类垃圾箱.为了了解垃圾分类的效果,该小区物业随机抽取了200位居民进行问卷调查,每位居民对小区采取的措施给出“满意”或“不满意”的评价.根据调查结果统计并做出年龄分布条形图和持不满意态度的居民的结构比例图,如图,在这200份问卷中,持满意态度的频率是0.65.
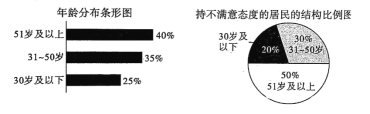
(1)完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异
的把握认为“51岁及以上”和“50岁及以下”的居民对该小区采取的措施的评价有差异
满意 | 不满意 | 总计 | |
51岁及以上的居民 | |||
50岁及以下的居民 | |||
总计 | 200 |
(2)按“51岁及以上”和“50岁及以下”的年龄段采取分层抽样的方法从中随机抽取5份,再从这5份调查问卷中随机抽取2份进行电话家访,求电话家访的两位居民恰好一位年龄在51岁及以上,另一位年龄在50岁及以下的概率.
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附表及参考公式: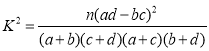 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义城为R的函数![]() ,若满足:①
,若满足:①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() 且
且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.下列函数是“偏对称函数”的是( )
为“偏对称函数”.下列函数是“偏对称函数”的是( )
A.![]() B.
B.![]()
C.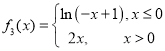 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
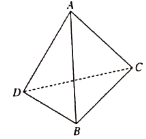
【题目】现有一副斜边长为10的直角三角板,将它们斜边![]() 重合,若将其中一个三角板沿斜边折起形成三棱锥
重合,若将其中一个三角板沿斜边折起形成三棱锥![]() ,如图所示,已知
,如图所示,已知![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为______;该三棱锥体积的最大值为_______.
的外接球的表面积为______;该三棱锥体积的最大值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com