
【题目】线段AB为圆O的直径,点E,F在圆O上,AB//EF,矩形ABCD所在平面和圆O所在平面垂直,且![]() .则( )
.则( )
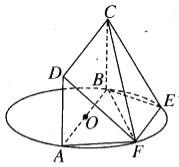
A.DF//平面BCE
B.异面直线BF与DC所成的角为30°
C.△EFC为直角三角形
D.![]()
【答案】BD
【解析】
四边形![]() 确定一个平面,
确定一个平面,![]() 不平行,说明
不平行,说明![]() 与平面
与平面![]() 有公共点,从而判断A选项;
有公共点,从而判断A选项;
连接![]() ,
,![]() 交
交![]() 于点
于点![]() ,根据题设条件得出
,根据题设条件得出![]() 为等边三角形,异面直线BF与DC所成的角为
为等边三角形,异面直线BF与DC所成的角为![]() ,从而判断B选项;
,从而判断B选项;
求出![]() 三边的边长,根据勾股定理判断C选项;
三边的边长,根据勾股定理判断C选项;
根据棱锥的体积公式得出![]() ,即可判断D选项.
,即可判断D选项.
对A项,因为![]() ,
,![]() ,所以四边形
,所以四边形![]() 确定一个平面
确定一个平面
由于![]() 长度不相等,则
长度不相等,则![]() 不平行,即
不平行,即![]() 与平面
与平面![]() 有公共点,故A错误;
有公共点,故A错误;
对B项,连接![]() ,
,![]() 交
交![]() 于点
于点![]()
因为![]() ,
,![]() ,所以四边形
,所以四边形![]() 为菱形
为菱形
则![]() ,所以
,所以![]() 为等边三角形
为等边三角形
由于点![]() 为
为![]() 的中点,则
的中点,则![]()
因为![]() ,所以异面直线BF与DC所成的角为
,所以异面直线BF与DC所成的角为![]() ,故B正确;
,故B正确;
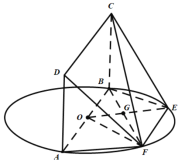
对C项,由于四边形![]() 为菱形,则
为菱形,则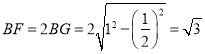
由面面垂直的性质以及线面垂直的性质可知,![]()
所以![]()
又![]() ,所以
,所以![]() 不是直角三角形,故C错误;
不是直角三角形,故C错误;
对D项,因为![]() ,
,![]() ,
,![]() ,所以
,所以
由面面垂直的性质可知,![]() 平面
平面![]() ,所以
,所以![]()
过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]()
根据面面垂直的性质可知![]() 平面
平面![]()
则![]()
即![]() ,故D正确;
,故D正确;

故选:BD


科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,已知公差
中,已知公差![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求![]() .
.
【答案】(1)![]() ;(2)100
;(2)100
【解析】试题分析:(1)根据题意![]() ,
, ![]() ,
, ![]() 成等比数列得
成等比数列得![]() 得
得![]() 求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得
求出d即可得通项公式;(2)求项的绝对前n项和,首先分清数列有多少项正数项和负数项,然后正数项绝对值数值不变,负数项绝对值要变号,从而得![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,∴
,∴![]()
![]()
![]()
![]() 计算 即可得出结论
计算 即可得出结论
解析:(1)由题意可得,则![]() ,
, ![]() ,
,
![]() ,即
,即![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
(2)由(1)得![]() 时,
时,
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() .
.
∴![]() .
.
点睛:对于数列第一问首先要熟悉等差和等比通项公式及其性质即可轻松解决,对于第二问前n项的绝对值的和问题,首先要找到数列由多少正数项和负数项,进而找到绝对值所影响的项,然后在求解即可得结论
【题型】解答题
【结束】
18
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为直径的圆
为直径的圆![]() .当
.当![]() 时,圆
时,圆![]() 的半径为2.
的半径为2.
(1)求![]() 的方程;
的方程;
(2)已知点![]() ,对任意的斜率
,对任意的斜率![]() ,圆
,圆![]() 上是否总存在点
上是否总存在点![]() 满足
满足![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,以下结论:
上的动点,以下结论:
①![]() 平面
平面![]() ;
;
②![]() ;
;
③三棱锥![]() ,体积不变;
,体积不变;
④![]() 为
为![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大.
所成角最大.
其中正确的序号为( )
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某病毒研究所为了研究温度对某种病毒的影响,在温度t(℃)逐渐升高时,连续测20次病毒的活性指标值y,实验数据处理后得到下面的散点图,将第1~14组数据定为A组,第15~20组数据定为B组.
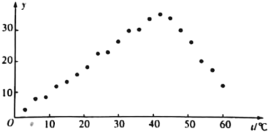
(Ⅰ)某研究员准备直接根据全部20组数据用线性回归模型拟合y与t的关系,你认为是否合理?请从统计学的角度简要说明理由.
(Ⅱ)若根据A组数据得到回归模型![]() ,根据B组数据得到回归模型
,根据B组数据得到回归模型![]() ,以活性指标值大于5为标准,估计这种病毒适宜生存的温度范围(结果精确到0.1).
,以活性指标值大于5为标准,估计这种病毒适宜生存的温度范围(结果精确到0.1).
(Ⅲ)根据实验数据计算可得:A组中活性指标值的平均数![]() ,方差
,方差![]()
![]() ;B组中活性指标值的平均数
;B组中活性指标值的平均数![]() ,方差
,方差![]() .请根据以上数据计算全部20组活性指标值的平均数
.请根据以上数据计算全部20组活性指标值的平均数![]() 和方差
和方差![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 交于M,抛物线C的焦点为F,且
交于M,抛物线C的焦点为F,且![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设点Q是抛物线C上的动点,点D,E在y轴上,圆![]() 内切于三角形
内切于三角形![]() ,求三角形
,求三角形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 底面
底面![]() .
.
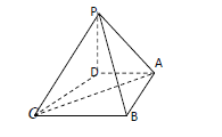
(1)在线段![]() 上是否存在一点F,使得
上是否存在一点F,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,试说明理由;
的值;若不存在,试说明理由;
(2)在(1)的条件下,若![]() 与
与![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
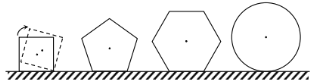
【题目】现有边长均为1的正方形正五边形正六边形及半径为1的圆各一个,在水平桌面上无滑动滚动一周,它们的中心的运动轨迹长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com