
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,曲线
,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)设 ![]() 为参数,若
为参数,若 ![]() ,求直线
,求直线 ![]() 的参数方程;
的参数方程;
(2)已知直线 ![]() 与曲线
与曲线 ![]() 交于
交于 ![]() ,设
,设 ![]() ,且
,且 ![]() ,求实数
,求实数 ![]() 的值.
的值.
【答案】
(1)解:直线 ![]() 的极坐标方程为
的极坐标方程为 ![]()
所以 ![]() ,即
,即 ![]()
因为 ![]() 为参数,若
为参数,若 ![]() ,代入上式得
,代入上式得 ![]() ,
,
所以直线 ![]() 的参数方程为
的参数方程为 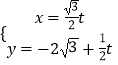 (
( ![]() 为参数)
为参数)
(2)解:由 ![]() ,得
,得 ![]()
由 ![]() 代入,得
代入,得 ![]()
将直线 ![]() 的参数方程与
的参数方程与 ![]() 的直角坐标方程联立
的直角坐标方程联立
得 ![]() (*)
(*)![]()
![]() ,
,
设点 ![]() 分别对应参数
分别对应参数 ![]() 恰为上述方程的根
恰为上述方程的根
则 ![]() ,
,
由题设得 ![]() ,
,
则有 ![]() ,得
,得 ![]() 或
或 ![]()
因为 ![]() ,所以
,所以 ![]() .
.
【解析】(1)直线l的极坐标方程为![]() ,利用互化公式可得直角坐标方程:
,利用互化公式可得直角坐标方程:![]() 设t为参数,即可得出直线l的参数方程,(2)把直线l的参数方程与C的直角坐标方程联立,利用t的几何意义可解得实数a的值.
设t为参数,即可得出直线l的参数方程,(2)把直线l的参数方程与C的直角坐标方程联立,利用t的几何意义可解得实数a的值.
【考点精析】本题主要考查了极坐标系的相关知识点,需要掌握平面内取一个定点O,叫做极点;自极点O引一条射线OX叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系才能正确解答此题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】某人到甲、乙两市各 ![]() 个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )
个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )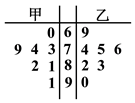
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
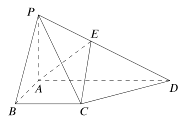
【题目】如图,在四棱锥 ![]() 中,底面
中,底面 ![]() 为直角梯形,
为直角梯形, ![]() ,且
,且 ![]() ,
, ![]() 平面
平面 ![]() .
.
(1)求 ![]() 与平面
与平面 ![]() 所成角的正弦值;
所成角的正弦值;
(2)棱 ![]() 上是否存在一点
上是否存在一点 ![]() 满足
满足 ![]() ?若存在,求
?若存在,求 ![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于椭圆 ![]() ,有如下性质:若点
,有如下性质:若点 ![]() 是椭圆上的点,则椭圆在该点处的切线方程为
是椭圆上的点,则椭圆在该点处的切线方程为 ![]() .利用此结论解答下列问题.
.利用此结论解答下列问题.
(Ⅰ)求椭圆 ![]() 的标准方程;
的标准方程;
(Ⅱ)若动点 ![]() 在直线
在直线 ![]() 上,经过点
上,经过点 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 相切,切点分别为
相切,切点分别为 ![]() .求证直线
.求证直线 ![]() 必经过一定点.
必经过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (
( ![]() )在同一半周期内的图象过点
)在同一半周期内的图象过点 ![]() ,
, ![]() ,
, ![]() ,其中
,其中 ![]() 为坐标原点,
为坐标原点, ![]() 为函数
为函数 ![]() 图象的最高点,
图象的最高点, ![]() 为函数
为函数 ![]() 的图象与
的图象与 ![]() 轴的正半轴的交点,
轴的正半轴的交点, ![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求 ![]() 的值;
的值;
(2)将 ![]() 绕原点
绕原点 ![]() 按逆时针方向旋转角
按逆时针方向旋转角 ![]() ,得到
,得到 ![]() ,若点
,若点 ![]() 恰好落在曲线
恰好落在曲线 ![]() (
( ![]() )上(如图所示),试判断点
)上(如图所示),试判断点 ![]() 是否也落在曲线
是否也落在曲线 ![]() (
( ![]() )上,并说明理由.
)上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系 ![]() 中,直线
中,直线 ![]() 过
过 ![]() ,倾斜角为
,倾斜角为 ![]() .以
.以 ![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(Ⅰ)求直线 ![]() 的参数方程和曲线
的参数方程和曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线 ![]() 与曲线
与曲线 ![]() 交于
交于 ![]() 、
、 ![]() 两点,且
两点,且 ![]() ,求直线
,求直线 ![]() 的斜率
的斜率 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,分别求函数
时,分别求函数![]() 的最小值和
的最小值和![]() 的最大值,并证明当
的最大值,并证明当![]() 时,
时, ![]() 成立;
成立;
(3)令![]() ,当
,当![]() 时,判断函数
时,判断函数![]() 有几个不同的零点并证明.
有几个不同的零点并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com