
°æƒø°øƒ≥π§≥ß…˙≤˙“ª÷÷“«∆˜µƒ‘™º˛£¨”…”⁄ Ð…˙≤˙ƒÐ¡¶∫Õºº ıÀÆ∆ΩµƒœÞ÷∆£¨ª·≤˙…˙“ª–©¥Œ∆∑£¨∏˘æðæ≠—È÷™µ¿£¨∆‰¥Œ∆∑¬ ![]() ”λ’≤˙¡ø
”λ’≤˙¡ø![]() £®ÕÚº˛£©÷ƺ‰¬˙◊„πÿœµ£∫
£®ÕÚº˛£©÷ƺ‰¬˙◊„πÿœµ£∫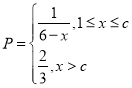 £®
£®![]() £©“—÷™√ø…˙≤˙1ÕÚº˛∫œ∏Òµƒ“«∆˜ø…“‘”Ø¿˚2ÕÚ‘™£¨µ´√ø…˙≤˙1ÕÚº˛¥Œ∆∑Ω´ø˜À1ÕÚ‘™£¨π ≥ß∑Ωœ£Õ˚∂®≥ˆ∫œ µƒ»’≤˙¡ø.£®◊¢£∫¥Œ∆∑¬ =¥Œ∆∑ ˝/…˙≤˙¡ø£©
£©“—÷™√ø…˙≤˙1ÕÚº˛∫œ∏Òµƒ“«∆˜ø…“‘”Ø¿˚2ÕÚ‘™£¨µ´√ø…˙≤˙1ÕÚº˛¥Œ∆∑Ω´ø˜À1ÕÚ‘™£¨π ≥ß∑Ωœ£Õ˚∂®≥ˆ∫œ µƒ»’≤˙¡ø.£®◊¢£∫¥Œ∆∑¬ =¥Œ∆∑ ˝/…˙≤˙¡ø£©
£®1£© ‘Ω´…˙≤˙’‚÷÷“«∆˜‘™º˛√øÃϵƒ”Ø¿˚∂Ó![]() £®ÕÚ‘™£©±Ì 挙»’≤˙¡ø
£®ÕÚ‘™£©±Ì 挙»’≤˙¡ø![]() £®ÕÚº˛£©µƒ∫Ø ˝£ª
£®ÕÚº˛£©µƒ∫Ø ˝£ª
£®2£©µ±»’≤˙¡øŒ™∂ý…Ÿ ±£¨ø…ªÒµ√◊Ó¥Û¿˚»Û£ø
°æ¥∞∏°ø£®1£©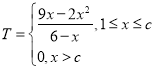 £®2£©3ÕÚº˛
£®2£©3ÕÚº˛
°æΩ‚Œˆ°ø
£®1£©√øÃϵƒ”Æ¿˚Œ™T£Ω»’≤˙¡ø£®x£©°¡’˝∆∑¬ £®1©ÅP£©°¡2©Å»’≤˙¡ø£®x£©°¡¥Œ∆∑¬ £®P£©°¡1£¨∏˘æð∑÷∂Œ∫Ø ˝∑÷∂Œ—–æø£¨’˚¿Ìº¥ø…£ª
£®2£©¿˚”√ª˘±æ≤ªµ» Ω£¨«Û∫Ø ˝µƒ◊Ó¥Û÷µ£Æ
£®1£©µ±x£æc ±£¨P![]() £¨
£¨
°ýT![]() x2
x2![]() x1£Ω0
x1£Ω0
µ±1°Ðx°Ðc ±£¨![]() £¨
£¨
°ý![]()
◊€…œ£¨»’”Ø¿˚∂ÓT£®ÕÚ‘™£©”λ’≤˙¡øx£®ÕÚº˛£©µƒ∫Ø ˝πÿœµŒ™£∫
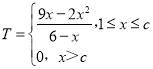
£®2£©”…£®1£©÷™£¨µ±x£æc ±£¨√øÃϵƒ”Ø¿˚∂ÓŒ™0
µ±1°Ðx°Ðc£¨”÷3°Ðc°Ð6£¨¥À ±£¨T![]() 15©Å2[£®6©Åx£©
15©Å2[£®6©Åx£©![]() ]°Ð15©Å12£Ω3
]°Ð15©Å12£Ω3
µ±«“Ωˆµ±x£Ω3 ±»°µ»∫≈
°ýTmax£Ω3£¨¥À ±x£Ω3
À˘“‘µ±»’≤˙¡øŒ™3ÕÚº˛ ±£¨ø…ªÒµ√◊Ó¥Û¿˚»Û.


 ”≈º”æ´æÌœµ¡–¥∞∏
”≈º”æ´æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…ËÕ÷‘≤![]() (a>b>0)µƒ◊ÛΩπµ„Œ™F£¨…œ∂•µ„Œ™B. “—÷™Õ÷‘≤µƒ¿Î–ƒ¬ Œ™
(a>b>0)µƒ◊ÛΩπµ„Œ™F£¨…œ∂•µ„Œ™B. “—÷™Õ÷‘≤µƒ¿Î–ƒ¬ Œ™![]() £¨µ„Aµƒ◊¯±ÍŒ™
£¨µ„Aµƒ◊¯±ÍŒ™![]() £¨«“
£¨«“![]() .
.
£®I£©«ÛÕ÷‘≤µƒ∑Ω≥ãª
£®II£©…Ë÷±œþl£∫ ![]() ”ÎÕ÷‘≤‘⁄µ⁄“ªœÛœÞµƒΩªµ„Œ™P£¨«“l”Î÷±œþABΩª”⁄µ„Q. »Ù
”ÎÕ÷‘≤‘⁄µ⁄“ªœÛœÞµƒΩªµ„Œ™P£¨«“l”Î÷±œþABΩª”⁄µ„Q. »Ù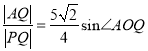 (OŒ™‘≠µ„) £¨«Ûkµƒ÷µ.
(OŒ™‘≠µ„) £¨«Ûkµƒ÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂![]() ÷–£¨∆Ω√Ê
÷–£¨∆Ω√Ê![]() ∆Ω√ÊABCD£¨
∆Ω√ÊABCD£¨![]() «µ»±þ»˝Ω«–Œ£¨Àƒ±þ–ŒABCD «æÿ–Œ£¨
«µ»±þ»˝Ω«–Œ£¨Àƒ±þ–ŒABCD «æÿ–Œ£¨![]() £¨FŒ™¿‚PA…œ“ªµ„£¨«“
£¨FŒ™¿‚PA…œ“ªµ„£¨«“![]() £¨MŒ™ADµƒ÷–µ„£¨Àƒ¿‚◊∂
£¨MŒ™ADµƒ÷–µ„£¨Àƒ¿‚◊∂![]() µƒÃª˝Œ™
µƒÃª˝Œ™![]() £Æ
£Æ
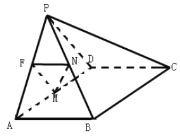
£®1£©»Ù![]() £¨N «PBµƒ÷–µ„£¨«Û÷§£∫∆Ω√Ê
£¨N «PBµƒ÷–µ„£¨«Û÷§£∫∆Ω√Ê![]() ∆Ω√ÊPCD£ª
∆Ω√ÊPCD£ª
£®2£©‘⁄£®¢Ò£©µƒÃıº˛£¨«Û»˝¿‚◊∂![]() µƒÃª˝£Æ
µƒÃª˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ù¥Ê‘⁄ µ ˝![]() πµ√
πµ√![]() ‘Ú≥∆
‘Ú≥∆![]() ««¯º‰
««¯º‰![]() µƒ
µƒ![]() “ªƒ⁄µ„£Æ
“ªƒ⁄µ„£Æ
£®1£©«Û÷§£∫![]() µƒ≥‰“™Ãıº˛ «¥Ê‘⁄
µƒ≥‰“™Ãıº˛ «¥Ê‘⁄![]() πµ√
πµ√![]() ««¯º‰
««¯º‰![]() µƒ
µƒ![]() “ªƒ⁄µ„£ª
“ªƒ⁄µ„£ª
£®2£©»Ù µ ˝![]() ¬˙◊„£∫
¬˙◊„£∫![]() «Û÷§£∫¥Ê‘⁄
«Û÷§£∫¥Ê‘⁄![]() £¨ πµ√
£¨ πµ√![]() ««¯º‰
««¯º‰![]() µƒ
µƒ![]() “ªƒ⁄µ„£ª
“ªƒ⁄µ„£ª
£®3£©∏¯∂® µ ˝![]() £¨»Ù∂‘”⁄»Œ“‚«¯º‰
£¨»Ù∂‘”⁄»Œ“‚«¯º‰![]() £¨
£¨![]() ««¯º‰µƒ
««¯º‰µƒ![]() “ªƒ⁄µ„£¨
“ªƒ⁄µ„£¨![]() ««¯º‰µƒ
««¯º‰µƒ![]() “ªƒ⁄µ„£¨«“≤ªµ» Ω
“ªƒ⁄µ„£¨«“≤ªµ» Ω![]() ∫Õ≤ªµ» Ω
∫Õ≤ªµ» Ω![]() ∂‘”⁄»Œ“‚
∂‘”⁄»Œ“‚![]() ∂º∫„≥…¡¢£¨«Û÷§£∫
∂º∫„≥…¡¢£¨«Û÷§£∫![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄Àƒ¿‚◊∂![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() .
.

£®1£©»Ùµ„![]() Œ™
Œ™![]() µƒ÷–µ„£¨«Û÷§£∫
µƒ÷–µ„£¨«Û÷§£∫![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©µ±∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() ±£¨«Û∂˛√ÊΩ«
±£¨«Û∂˛√ÊΩ«![]() µƒ”ýœ“÷µ.
µƒ”ýœ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–![]() ¬˙◊„
¬˙◊„![]() £¨«“
£¨«“![]()
£®1£©«Û ˝¡–![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
£®2£©«Û ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ
œÓ∫Õ![]() £ª
£ª
£®3£©»Ù![]() £¨«Û÷§
£¨«Û÷§![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() £¨
£¨ ![]() Œ™¡ΩÃı≤ªÕ¨µƒ÷±œþ£¨
Œ™¡ΩÃı≤ªÕ¨µƒ÷±œþ£¨ ![]() £¨
£¨ ![]() Œ™¡Ω∏ˆ≤ªÕ¨µƒ∆Ω√Ê£¨∂‘”⁄œ¬¡–Àƒ∏ˆ√¸Ã‚£∫
Œ™¡Ω∏ˆ≤ªÕ¨µƒ∆Ω√Ê£¨∂‘”⁄œ¬¡–Àƒ∏ˆ√¸Ã‚£∫
¢Ÿ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() ¢⁄
¢⁄![]() £¨
£¨ ![]()
¢€![]() £¨
£¨ ![]() £¨
£¨ ![]() ¢Ð
¢Ð![]() £¨
£¨ ![]()
∆‰÷–’˝»∑√¸Ã‚µƒ∏ˆ ˝”–£® £©
A. ![]() ∏ˆ B.
∏ˆ B. ![]() ∏ˆ C.
∏ˆ C. ![]() ∏ˆ D.
∏ˆ D. ![]() ∏ˆ
∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø«ð¡˜∏–“ª÷±‘⁄Õ˛–≤Œ“√«µƒ…˙ªÓ£¨ƒ≥º≤≤°øÿ÷∆÷––ƒŒ™¡À—–æø«ð¡˜∏–≤°∂æ∑±÷≥∏ˆ ˝![]() £®∏ˆ£©ÀÊ ±º‰
£®∏ˆ£©ÀÊ ±º‰![]() £®ÃÏ£©±‰ªØµƒπʬ…£¨ ’ºØ ˝æð»Áœ¬£∫
£®ÃÏ£©±‰ªØµƒπʬ…£¨ ’ºØ ˝æð»Áœ¬£∫
ÃÏ ˝ | 1 | 2 | 3 | 4 | 5 | 6 |
∑±÷≥∏ˆ ˝ | 6 | 12 | 25 | 49 | 95 | 190 |
◊˜≥ˆ…¢µ„Õºø…ø¥≥ˆ—˘±æµ„∑÷≤º‘⁄“ªÃı÷∏ ˝–Õ∫Ø ˝![]() µƒ÷ÐŒß.
µƒ÷ÐŒß.
±£¡Ù–° ˝µ„∫Û¡ΩŒª ˝µƒ≤Œøº ˝æð£∫
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨∆‰÷–
£¨∆‰÷–![]()
£®1£©«Û≥ˆ![]() πÿ”⁄
πÿ”⁄![]() µƒªÿπÈ∑Ω≥ã®±£¡Ù–° ˝µ„∫Û¡ΩŒª ˝◊÷£©£ª
µƒªÿπÈ∑Ω≥ã®±£¡Ù–° ˝µ„∫Û¡ΩŒª ˝◊÷£©£ª
£®2£©“—÷™![]() £¨π¿À„µ⁄ÀƒÃϵƒ≤–≤Ó.
£¨π¿À„µ⁄ÀƒÃϵƒ≤–≤Ó.
≤Œøºπ´ Ω£∫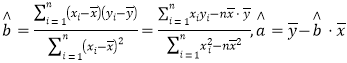
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄’˝∑ΩÃÂ![]() ÷–£¨µ„
÷–£¨µ„![]() £¨
£¨![]() ∑÷± «
∑÷± «![]() £¨
£¨![]() µƒ÷–µ„£¨‘Úœ¬¡–Àµ∑®’˝»∑µƒ «£® £©
µƒ÷–µ„£¨‘Úœ¬¡–Àµ∑®’˝»∑µƒ «£® £©
A. ![]() B.
B. ![]() ”Î
”Î![]() À˘≥…Ω«Œ™
À˘≥…Ω«Œ™![]()
C. ![]() ∆Ω√Ê
∆Ω√Ê![]() D.
D. ![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…Ω«µƒ”ýœ“÷µŒ™
À˘≥…Ω«µƒ”ýœ“÷µŒ™![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com