
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三个点在椭圆
中恰有三个点在椭圆![]() 上,左、右焦点分别为
上,左、右焦点分别为![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过左焦点![]() 且不与坐标轴平行的直线
且不与坐标轴平行的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,若线段
两点,若线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用椭圆的对称性确定在椭圆上的三点,由椭圆的上顶点![]() 可求出a,点
可求出a,点![]() 或
或![]() 的坐标代入椭圆求出b,即可写出椭圆的方程;(2)联立直线
的坐标代入椭圆求出b,即可写出椭圆的方程;(2)联立直线![]() 的方程与椭圆方程得关于x的一元二次方程,利用韦达定理求出两根之和与两根之积,即可利用弦长公式求出
的方程与椭圆方程得关于x的一元二次方程,利用韦达定理求出两根之和与两根之积,即可利用弦长公式求出![]() ,求出点N的坐标即可写出直线
,求出点N的坐标即可写出直线![]() 的垂直平分线的方程,令
的垂直平分线的方程,令![]() 求出
求出![]() ,代入
,代入![]() 得到关于k的分式,利用基本不等式可求得最小值.
得到关于k的分式,利用基本不等式可求得最小值.
(1)易知![]() ,
,![]() 关于
关于![]() 轴对称,一定都在椭圆上,所以
轴对称,一定都在椭圆上,所以![]() 一定不在椭圆上,根据题意
一定不在椭圆上,根据题意![]() 也在椭圆上,则
也在椭圆上,则![]() ,
,
将![]() 代入椭圆方程得
代入椭圆方程得![]() ,
,
所以椭圆方程为![]() .
.
(2)由![]() 知椭圆的左焦点
知椭圆的左焦点![]() ,
,
设直线![]() 的方程为
的方程为![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .
.
联立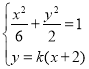 ,可得
,可得![]() ,
,
则![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
点![]()
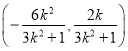 ,
,
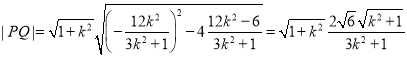
![]() ,
,
![]() 垂直平分线方程为:
垂直平分线方程为:![]() ,
,
令![]() ,求得
,求得![]() ,则
,则![]() ,
,
所以![]()
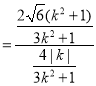
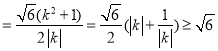 ,当且仅当
,当且仅当![]() 即
即![]() 时取等号,
时取等号,
因此,当![]() ,
,![]() 取最小值
取最小值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() 分别为
分别为![]() 内角
内角![]() 的对边,若
的对边,若![]() 是锐角三角形,需要同时满足下列四个条件中的三个:
是锐角三角形,需要同时满足下列四个条件中的三个:
①![]() ②
②![]() ③
③![]() ④
④![]()
(1)条件①④能否同时满足,请说明理由;
(2)以上四个条件,请在满足三角形有解的所有组合中任选一组,并求出对应的![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py(p>0),F为抛物线C的焦点.以F为圆心,p为半径作圆,与抛物线C在第一象限交点的横坐标为2.
(1)求抛物线C的方程;
(2)直线y=kx+1与抛物线C交于A,B两点,过A,B分别作抛物线C的切线l1,l2,设切线l1,l2的交点为P,求证:△PAB为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年女排世界杯(第13届女排世界杯)是由国际排联![]() 举办的赛事,比赛于2019年9月14日至9月29日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球
举办的赛事,比赛于2019年9月14日至9月29日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球![]() _
_![]() ,已知这种球的质量指标ξ(单位:
,已知这种球的质量指标ξ(单位:![]() )服从正态分布
)服从正态分布![]() .比赛赛制采取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以
.比赛赛制采取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以![]() 或
或![]() 取胜的球队积3分,负队积0分;而在比赛中以
取胜的球队积3分,负队积0分;而在比赛中以![]() 取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为
取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为![]() .
.
(1)如果比赛准备了1000个排球,估计质量指标在![]() 内的排球个数(计算结果取整数)
内的排球个数(计算结果取整数)
(2)第10轮比赛中,记中国队![]() 取胜的概率为
取胜的概率为![]() ,求出
,求出![]() 的最大值点
的最大值点![]() ,并以
,并以![]() 作为p的值,解决下列问题.
作为p的值,解决下列问题.
(i)在第10轮比赛中,中国队所得积分为X,求X的分布列;
(ii)已知第10轮美国队积3分,判断中国队能否提前一轮夺得冠军(第10轮过后,无论最后一轮即第11轮结果如何,中国队积分最多)?若能,求出相应的概率;若不能,请说明理由.
参考数据:![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年春节期间全国流行在微信群里发抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如下:
金额分组 |
|
|
|
|
|
|
频 数 | 3 | 9 | 17 | 11 | 8 | 2 |
(1)求产生的手气红包的金额不小于9元的频率;
(2)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(3)在这50个红包组成的样本中,将频率视为概率.
①若红包金额在区间![]() 内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
②随机抽取手气红包金额在![]() 内的两名幸运者,设其手气金额分别为
内的两名幸运者,设其手气金额分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 的短轴的两个端点分别为
的短轴的两个端点分别为![]() 、
、![]() ,
,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 、
、![]() 的动点,且
的动点,且![]() 的面积最大值为
的面积最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点
作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点![]() 和点
和点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com