
【题目】如图,在三棱柱![]() 中,
中, ![]() ,顶点
,顶点![]() 在底面
在底面 ![]() 上的射影恰为点
上的射影恰为点 ![]() ,且
,且![]() .
.

(1)求棱 ![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(2)在棱 ![]() 上确定一点
上确定一点![]() ,使
,使![]() ,并求出二面角
,并求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:根据题意建立如图所示的空间直角坐标系,(1)求出![]() 与
与![]() ,所在直线的向量,利用向量的夹角公式即可求出结果,再根据异面直线成角的范围,即可求出结果;(2)平面
,所在直线的向量,利用向量的夹角公式即可求出结果,再根据异面直线成角的范围,即可求出结果;(2)平面![]() 和平面
和平面![]() 的法向量分别为m和n,即可求出二面角
的法向量分别为m和n,即可求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
试题解析:解(1)建立如图所示的空间直角坐标系,
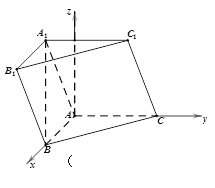
则C(0, 2, 0),B(2, 0 , 0),A1(0,-2, 2),B1(4, 0 , 2).从而, ![]() =(0,-2, 2),
=(0,-2, 2),![]() =(-2, 2, 0).
=(-2, 2, 0).
记![]() 与
与![]() 的夹角为θ,则有
的夹角为θ,则有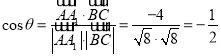 .
.
又由异面直线AA1与BC所成角的范围为(0,π),可得异面直线AA1与BC所成的角
为60. 4分
(2)记平面![]() 和平面
和平面![]() 的法向量分别为m和n,则由题设可令m=(x, y, z),且有平面
的法向量分别为m和n,则由题设可令m=(x, y, z),且有平面![]() 的法向量为n=(0,2,0).
的法向量为n=(0,2,0).
设![]() =(-2λ, 2λ, 0),则P(4-2λ, 2λ, 2).
=(-2λ, 2λ, 0),则P(4-2λ, 2λ, 2).
于是AP=![]() ,解得λ=
,解得λ=![]() 或λ=
或λ=![]() .
.
又题设可知λ∈(0, 1),则λ=![]() 舍去,故有λ=
舍去,故有λ=![]() .
.
从而,P为棱![]() 的中点,则坐标为P(3, 1, 2).
的中点,则坐标为P(3, 1, 2).
由平面PAB的法向量为m,故m⊥![]() 且m⊥
且m⊥![]() .
.
由m·![]() =0,即(x, y, z)·(3, 1 ,2)=0,解得3x+y+2z=0; ①
=0,即(x, y, z)·(3, 1 ,2)=0,解得3x+y+2z=0; ①
由m·![]() =0,即(x, y, z)·(-1,-1,-2)=0,解得-x-y-2z=0,②
=0,即(x, y, z)·(-1,-1,-2)=0,解得-x-y-2z=0,②
解方程①、②可得,x=0,y+2z=0,令y=-2,z=1,
则有m=(0,-2, 1) .
记平面PAB和平面ABA1所成的角为β,
则cosβ=![]() =
=![]()
故二面角![]() 的平面角的余弦值是
的平面角的余弦值是![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log ![]() 3),c=f(21.6),则a,b,c的大小关系是( )
3),c=f(21.6),则a,b,c的大小关系是( )
A.c<a<b
B.c<b<a
C.b<c<a
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点,焦点在x轴上的一椭圆与一双曲线有共同的焦点F1,F2,且|F1F2|=![]() ,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3∶7.
,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3∶7.
(1)求这两曲线的方程;
(2)若P为这两曲线的一个交点,求cos∠F1PF2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年9月16日05时,第19号台风“杜苏芮”的中心位于甲地,它以每小时30千米的速度向西偏北![]() 的方向移动,距台风中心
的方向移动,距台风中心![]() 千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受台风影响,则
千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受台风影响,则![]() 和
和![]() 的值分别为(附:
的值分别为(附: ![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市卫生防疫部门为了控制某种病毒的传染,提供了批号分别为![]() 的五批疫苗,供全市所辖的
的五批疫苗,供全市所辖的![]() 三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
(1)求三个区注射的疫苗批号中恰好有两个区相同的概率;
(2)记![]() 三个区选择的疫苗批号的中位数为
三个区选择的疫苗批号的中位数为![]() ,求
,求 ![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:实数x满足x2-5ax+4a2<0,其中a>0,命题q:实数x满足![]() .
.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某城市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80﹣2t(件),价格近似满足于  (元).
(元).
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
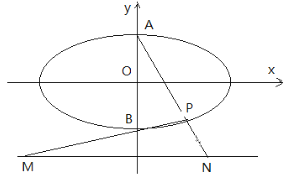
【题目】如图椭圆![]() 的上下顶点为A、B,直线
的上下顶点为A、B,直线![]() :
: ![]() ,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线
,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线![]() 于点N,连结BP并延长交直线
于点N,连结BP并延长交直线![]() 于点M,设AP、BP所在直线的斜率分别为
于点M,设AP、BP所在直线的斜率分别为![]() ,若椭圆的离心率为
,若椭圆的离心率为![]() ,且过点
,且过点![]() ,(1)求
,(1)求![]() 的值,并求
的值,并求![]() 最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com