
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 离心率为
离心率为![]() ,两准线之间的距离为8,点
,两准线之间的距离为8,点![]() 在椭圆
在椭圆![]() 上,且位于第一象限,过点
上,且位于第一象限,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 的交点
的交点![]() 在椭圆
在椭圆![]() 上,求点
上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由椭圆的离心率公式求得![]() ,由椭圆的准线方程
,由椭圆的准线方程![]() ,则
,则![]() ,即可求得
,即可求得![]() 和
和![]() 的值,则
的值,则![]() ,即可求得椭圆方程;(2)设
,即可求得椭圆方程;(2)设![]() 点坐标,分别求得直线
点坐标,分别求得直线![]() 的斜率及直线
的斜率及直线![]() 的斜率,则可求得
的斜率,则可求得![]() 及
及![]() 的斜率及方程,联立求得
的斜率及方程,联立求得![]() 点坐标,由
点坐标,由![]() 满足椭圆方程,求得
满足椭圆方程,求得![]() ,结合
,结合![]() 在椭圆E上,
在椭圆E上,![]() 联立即可求得
联立即可求得![]() 点坐标.
点坐标.
试题解析:(1)设椭圆的半焦距为c.因为椭圆E的离心率为![]() ,两准线之间的距离为8,所以
,两准线之间的距离为8,所以![]() ,
,![]() ,解得
,解得![]() ,于是
,于是![]() ,因此椭圆E的标准方程是
,因此椭圆E的标准方程是![]() .
.
(2)由(1)知,![]() ,
,![]() .设
.设![]() ,因为
,因为![]() 为第一象
为第一象
限的点,故![]() .当
.当![]() 时,
时,![]() 与
与![]() 相交于
相交于![]() ,与题设不符.
,与题设不符.
当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
, ![]() 直线
直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
从而直线![]() 的方程
的方程![]() ,① 直线
,① 直线![]() 的方程
的方程![]() ,②
,②
由①②,解得![]() ,所以
,所以![]() .因为点
.因为点![]() 在椭圆上,由对称性,得
在椭圆上,由对称性,得![]() ,即
,即![]() 或
或![]() .又
.又![]() 在椭圆E上,故
在椭圆E上,故![]() .
.
由 ,解得
,解得![]() ;
;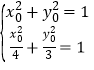 ,无解.因此点P的坐标为
,无解.因此点P的坐标为![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】为探索课堂教学改革,江门某中学数学老师用传统教学和“导学案”两种教学方式,在甲、乙两个平行班进行教学实验。为了解教学效果,期末考试后,分别从两个班级各随机抽取20名学生的成绩进行统计,得到如下茎叶图。记成绩不低于70分者为“成绩优良”。
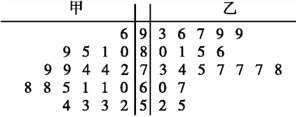
(Ⅰ)请大致判断哪种教学方式的教学效果更佳,并说明理由;
(Ⅱ)构造一个教学方式与成绩优良列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
(附:![]() ,其中
,其中![]() 是样本容量)
是样本容量)
独立性检验临界值表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了![]() 人,将调查情况进行整理后制成下表:
人,将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(![]() )完成被调查人员的频率分布直方图.
)完成被调查人员的频率分布直方图.
(![]() )若从年龄在
)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行追踪调查,求恰有
人进行追踪调查,求恰有![]() 人不赞成的概率.
人不赞成的概率.
(![]() )在
)在![]() 在条件下,再记选中的
在条件下,再记选中的![]() 人中不赞成“车辆限行”的人数为
人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
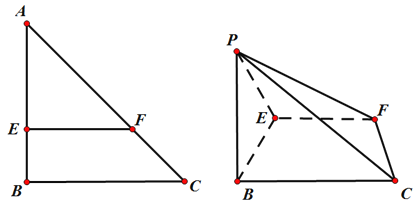
【题目】如图,在Rt![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 的大小为
的大小为![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 为线段
为线段![]() 的靠近
的靠近![]() 点的三等分点时,求
点的三等分点时,求![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 分别是角
分别是角![]() 的对边,已知
的对边,已知![]() ,现有以下判断:
,现有以下判断:
①![]() 不可能等于15; ②
不可能等于15; ②![]() ;
;
③作![]() 关于
关于![]() 的对称点
的对称点![]() 的最大值是
的最大值是![]() ;
;
④若![]() 为定点,则动点
为定点,则动点![]() 的轨迹围成的封闭图形的面积是
的轨迹围成的封闭图形的面积是![]() 。请将所有正确的判断序号填在横线上______________。
。请将所有正确的判断序号填在横线上______________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin 2x-
sin 2x-![]() cos2x.
cos2x.
(1)求f(x)的周期和最小值;
(2)将函数f(x)的图像上每一点的横坐标伸长到原来的两倍(纵坐标不变),再把所得图像上的所有点向上平移![]() 个单位,得到函数g(x)的图像,当
个单位,得到函数g(x)的图像,当![]() 时,求g(x)的值域.
时,求g(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com