
【题目】已知函数f(x)=|x|+|x﹣1|.
(1)若f(x)≥|m﹣1|恒成立,求实数m的最大值M;
(2)在(1)成立的条件下,正实数a,b满足a2+b2=M,证明:a+b≥2ab.
【答案】(1)2(2)见解析
【解析】
(1)求出函数的解析式,然后求解函数的最小值,通过|m﹣1|≤1,求解m的范围,得到m的最大值M.
(2)法一:综合法,利用基本不等式证明即可;法二:利用分析法,证明不等式成立的充分条件即可.
(1)由已知可得 ,
,
所以fmin(x)=1,
所以只需|m﹣1|≤1,解得﹣1≤m﹣1≤1,
∴0≤m≤2,
所以实数m的最大值M=2.
(2)法一:综合法
∵正实数a,b满足a2+b2=2,
∴ab≤1
∴![]() ,当且仅当a=b时取等号,①
,当且仅当a=b时取等号,①
又∴![]()
∴![]() ,当且仅当a=b时取等号,②
,当且仅当a=b时取等号,②
由①②得,
∴![]() ,
,
所以a+b≥2ab
法二:分析法因为a>0,b>0,
所以要证a+b≥2ab,只需证![]() ,
,
即证a2+b2+2ab≥4a2b2,
所以只要证2+2ab≥4a2b2,
即证2(ab)2-ab-1≤0,
即证![]() ,
,
因为2ab+1>0,
所以只需证ab≤1,
下证ab≤1,
因为2=a2+b2≥2ab,
所以ab≤1成立,
所以a+b≥2ab成立.


科目:高中数学 来源: 题型:
【题目】函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)在函数![]() 的图象上取
的图象上取![]() 两个不同的点,令直线
两个不同的点,令直线![]() 的斜率为
的斜率为![]() ,则在函数的图象上是否存在点
,则在函数的图象上是否存在点![]() ,且
,且![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 两点的坐标,若不存在,说明理由.
两点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l过点![]() 且倾斜角为
且倾斜角为![]() .以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为
.以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]() ,l与C交于M,N两点.
,l与C交于M,N两点.
(1)求C的直角坐标方程和![]() 的取值范围;
的取值范围;
(2)求MN中点H的轨迹的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有某种不透明充气包装的袋装零食,每袋零食附赠玩具A,B,C中的一个.对某零售店售出的100袋零食中附赠的玩具类型进行追踪调查,得到以下数据:
BBABC ACABA AAABC BABAA CAAAB
ABCCC BCBBC CABCA BACAB BCBCB
BCCCA BCCAA BCCCB ACCBB BACAB
ACCAB BBBAA CABCA BCBBC CABCA
(1)能否认为购买一袋该零食,获得玩具A,B,C的概率相同?请说明理由;
(2)假设每袋零食随机附赠玩具A,B,C是等可能的,某人一次性购买该零食3袋,求他能从这3袋零食中集齐玩具A,B及C的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
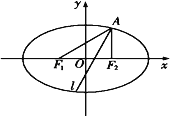
【题目】如图所示,已知椭圆E经过点![]() ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点![]() ,
,![]() 在x轴上,离心率e
在x轴上,离心率e![]() .直线l是
.直线l是![]() 的平分线,则椭圆E的方程是_____,l所在的直线方程是_____.
的平分线,则椭圆E的方程是_____,l所在的直线方程是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
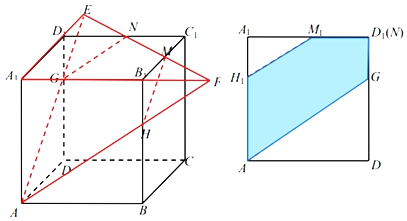
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 只有一个公共点,点
只有一个公共点,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程;
的方程;
(2)①若![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
②若![]() 是抛物线
是抛物线![]() 上与原点不重合的定点,且
上与原点不重合的定点,且![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数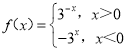 ,若
,若![]() ,b=f(log24.2),c=f(20.7),则a,b,c的大小关系为( )
,b=f(log24.2),c=f(20.7),则a,b,c的大小关系为( )
A.a<b<cB.b<a<cC.c<a<bD.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点的直线
的焦点的直线![]() 与抛物线交于
与抛物线交于![]() 两点,若
两点,若![]() 且
且![]() 中点的纵坐标为3.
中点的纵坐标为3.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的直线交抛物线于不同两点
的直线交抛物线于不同两点![]() ,分别过点
,分别过点![]() 、点
、点![]() 分别作抛物线
分别作抛物线![]() 的切线,所得的两条切线相交于点
的切线,所得的两条切线相交于点![]() .求
.求![]() 的面积的最小值及此时的直线的方程.
的面积的最小值及此时的直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com