
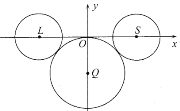
【题目】2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:![]() 是圆
是圆![]() 的圆心,圆
的圆心,圆![]() 过坐标原点
过坐标原点![]() ;点
;点![]() 、
、![]() 均在
均在![]() 轴上,圆
轴上,圆![]() 与圆
与圆![]() 的半径都等于2,圆
的半径都等于2,圆![]() 圆
圆![]() 均与圆
均与圆![]() 外切.已知直线
外切.已知直线![]() 过点
过点![]() .
.
(1)若直线![]() 与圆
与圆![]() 、圆
、圆![]() 均相切,则
均相切,则![]() 截圆
截圆![]() 所得弦长为__________;
所得弦长为__________;
(2)若直线![]() 截圆
截圆![]() 、圆
、圆![]() 、圆
、圆![]() 所得弦长均等于
所得弦长均等于![]() ,则
,则![]() __________.
__________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 至多只有一个公共点,求实数
至多只有一个公共点,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 的中点为
的中点为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前
的前![]() 项中的最大项为
项中的最大项为![]() ,最小项为
,最小项为![]() ,设
,设![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,
,![]() 点又恰为抛物线
点又恰为抛物线![]() 的焦点,以
的焦点,以![]() 为直径的圆与椭圆
为直径的圆与椭圆![]() 仅有两个公共点.
仅有两个公共点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,记点
两点,记点![]() ,
,![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,
,![]() ,
,![]() .直线
.直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,记
两点,记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() .
.
(ⅰ)证明:![]() 的周长为定值;
的周长为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在北宋1084年第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰.某图书馆中正好有这十本书现在小明同学从这十本书中任借两本阅读,那么他取到的书的书名中有“算”字的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附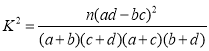 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1970年4月24日,我国发射了自己的第一颗人造地球卫星“东方红一号”,从此我国开始了人造卫星的新篇章.人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为![]() ,
,![]() ,下列结论正确的是( )
,下列结论正确的是( )
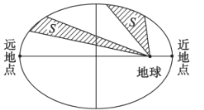
A.卫星向径的取值范围是![]()
B.卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间
C.卫星向径的最小值与最大值的比值越大,椭圆轨道越扁
D.卫星运行速度在近地点时最大,在远地点时最小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 的两顶点坐标
的两顶点坐标![]() ,
,![]() ,圆
,圆![]() 是
是![]() 的内切圆,在边
的内切圆,在边![]() ,
,![]() ,
,![]() 上的切点分别为
上的切点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
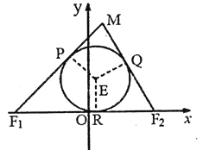
(Ⅰ)求证:![]() 为定值,并求出动点
为定值,并求出动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过![]() 的斜率不为零直线交曲线
的斜率不为零直线交曲线![]() 于
于![]() 、
、![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com