
【题目】在数列![]() 中,
中, ![]() 且
且![]() .
.
(1)求出![]() ,
,![]() ,
,![]() ;
;
(2)归纳猜想出数列![]() 的通项公式;
的通项公式;
(3)证明通项公式![]() .
.
【答案】(1)![]() ,
, ![]() ,
, ![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)依次代入n=1,2,3得![]() ,
, ![]() ,
, ![]() (2)根据分子规律得
(2)根据分子规律得![]() 1,由分母规律得
1,由分母规律得![]() ,即得数列
,即得数列![]() 的通项公式;(3)利用数学归纳法进行证明,由
的通项公式;(3)利用数学归纳法进行证明,由![]() 证明 n=k+1时成立.
证明 n=k+1时成立.
试题解析: (1)![]() ,
, ![]() ,
, ![]() (2)
(2)![]() (3)数学归纳法证明如下:
(3)数学归纳法证明如下:
(1)n=1时成立;(2)假设n=k成立,则![]() ,所以n=k+1时,
,所以n=k+1时, ![]() ,由(1)(2)得结论成立
,由(1)(2)得结论成立
点睛: 用数学归纳法证明等式的策略(1)用数学归纳法证明等式问题是常见题型,其关键点在于弄清等式两边的构成规律,等式两边各有多少项,以及初始值n0的值.(2)由n=k到n=k+1时,除考虑等式两边变化的项外还要充分利用n=k时的式子,即充分利用假设,正确写出归纳证明的步骤,从而使问题得以证明.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性、对称性等,请选择适当的探究顺序,研究函数![]() 的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
性质 | 理由 | 结论 | 得分 |
定义域 | |||
值域 | |||
奇偶性 | |||
周期性 | |||
单调性 | |||
对称性 | |||
作图 |
| ||
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在长为10千米的河流![]() 的一侧有一条观光带,观光带的前一部分为曲线段
的一侧有一条观光带,观光带的前一部分为曲线段![]() ,设曲线段
,设曲线段![]() 为函数
为函数![]() (单位:千米)的图象,且图象的最高点为
(单位:千米)的图象,且图象的最高点为![]() ;观光带的后一部分为线段
;观光带的后一部分为线段![]() .
.
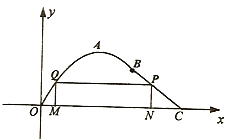
(1)求函数为曲线段![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)若计划在河流![]() 和观光带
和观光带![]() 之间新建一个如图所示的矩形绿化带
之间新建一个如图所示的矩形绿化带![]() ,绿化带仅由线段
,绿化带仅由线段![]() 构成,其中点
构成,其中点![]() 在线段
在线段![]() 上.当
上.当![]() 长为多少时,绿化带的总长度最长?
长为多少时,绿化带的总长度最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2(lnx+lna)(a>0).
(1)当a=1时,设函数g(x)= ![]() ,求函数g(x)的单调区间与极值;
,求函数g(x)的单调区间与极值;
(2)设f′(x)是f(x)的导函数,若 ![]() ≤1对任意的x>0恒成立,求实数a的取值范围;
≤1对任意的x>0恒成立,求实数a的取值范围;
(3)若x1 , x2∈( ![]() ,1),x1+x2<1,求证:x1x2<(x1+x2)4 .
,1),x1+x2<1,求证:x1x2<(x1+x2)4 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(万元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求:
(1)求![]() ; (2)线性回归方程
; (2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com