
【题目】函数![]() .
.
(1)根据![]() 不同取值,讨论函数
不同取值,讨论函数![]() 的奇偶性;
的奇偶性;
(2)若![]() ,对于任意的
,对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若已知![]() ,
,![]() . 设函数
. 设函数![]() ,
,![]() ,存在
,存在![]() 、
、![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)分![]() 和
和![]() 两种情况讨论,结合奇偶性的定义得出函数
两种情况讨论,结合奇偶性的定义得出函数![]() 的奇偶性;
的奇偶性;
(2)![]() 满足不等式
满足不等式![]() ,在
,在![]() 时,可得出
时,可得出![]() ,可得出不等式
,可得出不等式![]() 对任意的
对任意的![]() 恒成立,然后利用参变量分离法得出
恒成立,然后利用参变量分离法得出![]() ,利用函数单调性分别求出函数
,利用函数单调性分别求出函数![]() 和
和![]() 在区间
在区间![]() 上的最大值和最小值,即可得出实数
上的最大值和最小值,即可得出实数![]() 的取值范围;
的取值范围;
(3)由题意知,当![]() 时,
时,![]() ,将
,将![]() 代入函数
代入函数![]() 的解析式,求出该函数的最小值,利用复合函数法求出函数
的解析式,求出该函数的最小值,利用复合函数法求出函数![]() 在区间
在区间![]() 上的最大值,然后解不等式
上的最大值,然后解不等式![]() ,即可得出实数
,即可得出实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,关于原点对称.
,关于原点对称.
当![]() 时,
时,![]() ,
,![]() ,
,
此时,函数![]() 为奇函数;
为奇函数;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,此时,函数
,此时,函数![]() 为非奇非偶函数;
为非奇非偶函数;
(2)当![]() 时,则有
时,则有![]() 恒成立,此时
恒成立,此时![]() ;
;
当![]() 时,由
时,由![]() ,即
,即![]() ,即
,即![]() ,
,
![]() ,
,![]() ,则
,则![]() ,所以,不等式
,所以,不等式![]() 对任意的
对任意的![]() 恒成立,
恒成立,
由![]() ,即
,即![]() ,
,![]() ,即
,即![]() .
.
![]() 函数
函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() ,
,
函数![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,
,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)由题意知,当![]() 时,
时,![]() ,
,
当![]() 时,
时,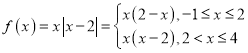 .
.
当![]() 时,
时,![]() ,
,
此时,函数![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
且![]() ,
,![]() ,则
,则![]() ;
;
当![]() 时,
时,![]() ,
,
此时,函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() .
.
所以,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
对于函数![]() ,
,
内层函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
外层函数![]() 是减函数,
是减函数,
所以,![]() ,
,
由题意得![]() ,则有
,则有![]() ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,写出
,写出![]() 所有可能的值;
所有可能的值;
(2)若数列![]() 是递增数列,且
是递增数列,且![]() 、
、![]() 、
、![]() 成等差数列,求p的值;
成等差数列,求p的值;
(3)若![]() ,且
,且![]() 是递增数列,
是递增数列,![]() 是递减数列,求数列
是递减数列,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学生假期参与志愿服务活动的情况,随机调查了![]() 名男生,
名男生,![]() 名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
超过 | 不超过 | |
男 |
|
|
女 |
|
|
(1)能否有![]() 的把握认为该校学生一周参与志愿服务活动时间是否超过
的把握认为该校学生一周参与志愿服务活动时间是否超过![]() 小时与性别有关?
小时与性别有关?
(2)以这![]() 名学生参与志愿服务活动时间超过
名学生参与志愿服务活动时间超过![]() 小时的频率作为该事件发生的概率,现从该校学生中随机抽查
小时的频率作为该事件发生的概率,现从该校学生中随机抽查![]() 名学生,试估计这
名学生,试估计这![]() 名学生中一周参与志愿服务活动时间超过
名学生中一周参与志愿服务活动时间超过![]() 小时的人数.
小时的人数.
附:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工程队共有500人,要建造一段6000米的高速公路,工程需要把500人分成两组,甲组的任务是完成一段4000米的软土地带,乙组的任务是完成剩下的2000米的硬土地带,据测算,软、硬土地每米的工程量是30工(工为计量单位)和40工.
(1)若平均分配两组的人数,分别计算两组完工的时间,并求出此时全队的筑路工期;
(2)如何分配两组的人数会使得全队的筑路工期最短?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为
(α为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为![]() ,直线l的极坐标方程为
,直线l的极坐标方程为![]() .
.
(1)求直线l的直角坐标方程与曲线C的普通方程;
(2)若Q是曲线C上的动点,M为线段PQ的中点,直线l上有两点A,B,始终满足|AB|=4,求△MAB面积的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次高三年级模拟考试中,数学试卷有一道满分10分的选做题,学生可以从A,B两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,作为下一步教学的参考依据,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001~900.
(1)若采用系统抽样法抽样,从编号为001~090的成绩中用简单随机抽样确定的成绩编号为025,求样本中所有成绩编号之和;
(2)若采用分层抽样,按照学生选择A题目或B题目,将成绩分为两层.已知该校高三学生有540人选做A题目,有360人选做B题目,选取的样本中,A题目的成绩平均数为5,方差为2,B题目的成绩平均数为5.5,方差为0.25.
(i)用样本估计该校这900名考生选做题得分的平均数与方差;
(ii)本选做题阅卷分值都为整数,且选取的样本中,A题目成绩的中位数和B题目成绩的中位数都是5.5.从样本中随机选取两个大于样本平均值的数据做进一步调查,求取到的两个成绩来自不同题目的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备,通过市场分析,全年需投入固定成本3000万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且 ,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
(1)求出2019年的利润![]() (万元)关于年产量x(百辆)的函数关系式;(利润=销售额
(万元)关于年产量x(百辆)的函数关系式;(利润=销售额![]() 成本)
成本)
(2)2019年产量为多少(百辆)时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com