
【题目】已知![]() 是定义域为
是定义域为![]() 的奇函数,且当
的奇函数,且当![]() 时,
时, ![]() ,设
,设![]() “
“![]() ”.
”.
(1)若![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)设![]() 集合
集合![]() 与集合
与集合![]() 的交集为
的交集为![]() ,若
,若![]() 为假,
为假, ![]() 为真,求实数
为真,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知可得,函数![]() 为
为![]() 上的奇函数、且为增函数,由命题
上的奇函数、且为增函数,由命题![]() 为真,则
为真,则![]() ,所以
,所以![]() ,从而解得
,从而解得![]() ;(2)由集合
;(2)由集合![]()
![]() ,若
,若![]() 为真,则
为真,则![]() ,因为“
,因为“![]() 为假,
为假, ![]() 为真”等价于“
为真”等价于“![]() 、
、![]() 一真一假”,因此若
一真一假”,因此若![]() 真
真![]() 假,则
假,则![]() ;若
;若![]() 假
假![]() 真,则
真,则![]() .从而可得,实数
.从而可得,实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:∵函数![]() 是奇函数,∴
是奇函数,∴![]() ,………………………………1分
,………………………………1分
∵当![]() 时,
时, ![]() ,
,
∴函数![]() 为
为![]() 上的增函数,……………………………………2分
上的增函数,……………………………………2分
∵![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,………………4分
,………………4分
若![]() 为真,则
为真,则![]() ,解得
,解得![]() .…………………………6分
.…………………………6分
(2)![]() ,………………………………7分
,………………………………7分
若![]() 为真,则
为真,则![]() ,………………………………8分
,………………………………8分
∵![]() 为假,
为假, ![]() 为真,
为真,
∴![]() 、
、![]() 一真一假,…………………………………………9分
一真一假,…………………………………………9分
若![]() 真
真![]() 假,则
假,则![]() ;………………………………10分
;………………………………10分
若![]() 假
假![]() 真,则
真,则![]() .……………………………………11分
.……………………………………11分
综上,实数![]() 的取值范围是
的取值范围是![]() .……………………12分
.……………………12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,公路![]() 围成的是一块顶角为
围成的是一块顶角为![]() 的角形耕地,其中
的角形耕地,其中![]() ,在该块土地中
,在该块土地中![]() 处有一小型建筑,经测量,它到公路
处有一小型建筑,经测量,它到公路![]() 的距离分别为
的距离分别为![]() ,现要过点
,现要过点![]() 修建一条直线公路
修建一条直线公路![]() ,将三条公路围成的区域
,将三条公路围成的区域![]() 建成一个工业园.
建成一个工业园.

(1)以![]() 为坐标原点建立适当的平面直角坐标系,并求出
为坐标原点建立适当的平面直角坐标系,并求出![]() 点的坐标;
点的坐标;
(2)三条公路围成的工业园区![]() 的面积恰为
的面积恰为![]() ,求公路
,求公路![]() 所在直线方程.
所在直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域存在实数
,若在定义域存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() (
(![]()
![]() ),试判断
),试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若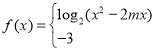
![]() 为其定义域上的“局部奇函数”,求实数
为其定义域上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,对于定义域内的任意实数
,对于定义域内的任意实数![]() ,有
,有![]() 成立,且
成立,且![]() 时,
时,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(3)已知![]() (实数
(实数![]() ),求实数
),求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 直角坐标方程;
直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图表示一位骑自行车者和一位骑摩托车者在相距![]() 的两城镇间旅行的函数图象,由图,可知骑自行车者用了
的两城镇间旅行的函数图象,由图,可知骑自行车者用了![]() ,沿途休息了
,沿途休息了![]() ,骑摩托车者用了
,骑摩托车者用了![]() ,根据这个图象,提出关于这两个旅行者的如下信息:
,根据这个图象,提出关于这两个旅行者的如下信息:

①骑自行车者比骑摩托车者早出发![]() ,晚到
,晚到![]() ;
;
②骑自行车者是变速运动,骑摩托者是匀速运动;
③骑摩托车者在出发了![]() 后,追上了骑自行车者.
后,追上了骑自行车者.
其中正确信息的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在自然数列中由1开始依次按如下规则将某些数染成红色.先染1;再染两个偶数2,4;再染4后最邻近的三个连续奇数5,7,9;再染9后最邻近的四个连续偶数10,12,14,16;再染此后最邻近的五个连续奇数17,19,21,23,25.按此规则一直染下去,得一红色子列1,2,4,5,7,9,10,12,14,16,17,….则红色子列中由1开始数起的第1996个数是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com