
【题目】如图所示,在斜三棱柱![]() 中,底面是等腰三角形,
中,底面是等腰三角形,![]() ,
,![]() 是
是![]() 的中点,侧面
的中点,侧面![]() 底面
底面![]() .
.
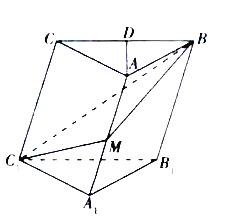
(1)求证:![]() ;
;
(2)过侧面![]() 的对角线
的对角线![]() 的平面交侧棱
的平面交侧棱![]() 于点
于点![]() ,若
,若![]() ,求证:截面
,求证:截面![]() 侧面
侧面![]() ;
;
(3)若截面![]() 平面
平面![]() ,
,![]() 成立吗?请说明理由.
成立吗?请说明理由.
【答案】(1)见解析; (2)见解析; (3)见解析.
【解析】
(1)根据面面垂直的性质证明![]() 侧面
侧面![]() ,即可证得;
,即可证得;
(2)延长![]() ,与
,与![]() 的延长线交于点N,证明
的延长线交于点N,证明![]() 侧面
侧面![]() 即可;
即可;
(3)过M作![]() 于点E,连接
于点E,连接![]() ,根据面面垂直的性质,
,根据面面垂直的性质,![]() 侧面
侧面![]() ,
,![]() ,结合长度关系即可得解.
,结合长度关系即可得解.
(1)证明:![]() ,D是
,D是![]() 的中点,
的中点,![]() .
.
∵底面![]() 侧面
侧面![]() ,底面
,底面![]() 侧面
侧面![]() ,
,![]() 底面
底面![]() ,
,
![]() 侧面
侧面![]() .
.
又![]() 侧面
侧面![]() ,
,![]() .
.
(2)证明:如图,延长![]() ,与
,与![]() 的延长线交于点N,
的延长线交于点N,
连接![]() ,则
,则![]() 平面
平面![]() ,
,

![]() ,
,![]() .
.![]() ,
,
![]() ,
,
![]() ,由已知侧面
,由已知侧面![]() 底面
底面![]()
所以侧面![]() 底面
底面![]() ,交线为
,交线为![]() ,
,
![]() 底面
底面![]() ,
,
![]() 侧面
侧面![]() ,
,![]() 平面
平面![]() ,
,
∴截面![]() 侧面
侧面![]() .
.
(3)成立.理由如下:
过M作![]() 于点E,连接
于点E,连接![]() .
.
∵截面![]() 侧面
侧面![]() ,根据面面垂直的性质,
,根据面面垂直的性质,
![]() 侧面
侧面![]() .
.
又![]() 侧面
侧面![]() ,
,![]() ,
,
![]() 四点共面.
四点共面.
![]() 侧面
侧面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() .
.
∴四边形![]() 是平行四边形,
是平行四边形,
又![]() ,
,![]() .
.
![]() 是
是![]() 的中点,
的中点,![]() ,
,
![]() .
.
![]() .
.


科目:高中数学 来源: 题型:
【题目】某学习小组通过对某商场一种品牌服装销售情况的调查发现:该服装在过去的一个月内(以![]() 天计),日销售量
天计),日销售量 ![]() (件)与时间x (天)的部分数据如下表所示,给出以下四种函数模型:①
(件)与时间x (天)的部分数据如下表所示,给出以下四种函数模型:① ![]() ,②
,② ![]() ,③
,③ ![]() ④
④![]() .请你根据上表中的数据,从中选择你认为最合适的一种函数来描述日销售量
.请你根据上表中的数据,从中选择你认为最合适的一种函数来描述日销售量![]() (件)与时间x(天)的变化关系,请将你选择的函数序号填写在横线上__________.(不需要求出具体解析式)
(件)与时间x(天)的变化关系,请将你选择的函数序号填写在横线上__________.(不需要求出具体解析式)
x (天) | 10 | 20 | 25 | 30 |
| 110 | 120 | 125 | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长均相等的四棱锥![]() 中,
中, ![]() 为底面正方形的中心,
为底面正方形的中心, ![]() ,
,![]() 分别为侧棱
分别为侧棱![]() ,
,![]() 的中点,有下列结论正确的有:( )
的中点,有下列结论正确的有:( )
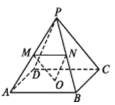
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学的![]() 名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐
名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐![]() 名同学(乘同一辆车的
名同学(乘同一辆车的![]() 名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的
名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的![]() 名同学中恰有
名同学中恰有![]() 名同学是来自于同一年级的乘坐方式共有_______种(有数字作答).
名同学是来自于同一年级的乘坐方式共有_______种(有数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法正确的是( )
A.若m∥α,n∥α,则 m∥n
B.若α⊥γ,β⊥γ,则α∥β
C.若m⊥α,n⊥β,且α⊥β,则m⊥n.
D.若m∥α,n∥α,且mβ, nβ,则α∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点A(2,6),且与直线l1: x+y-10=0相切于点B(6,4).
(1)求圆C的方程;
(2)过点P(6,24)的直线l2与圆C交于M,N两点,若△CMN为直角三角形,求直线l2的斜率;
(3)在直线l3: y=x-2上是否存在一点Q,过点Q向圆C引两切线,切点为E,F, 使△QEF为正三角形,若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,现有一组数据,将其绘制所得的茎叶图如图所示(其中茎为整数部分,叶为小数部分.例如:
,现有一组数据,将其绘制所得的茎叶图如图所示(其中茎为整数部分,叶为小数部分.例如:![]() 可记为
可记为![]() ,且上述数据的平均数为
,且上述数据的平均数为![]() .)
.)
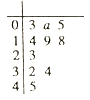
(Ⅰ)求茎叶图中数据![]() 的值;
的值;
(Ⅱ)现从茎叶图中小于![]() 的数据中任取两个数据分别替换
的数据中任取两个数据分别替换![]() 的值,求恰有一个数据使得函数没有零点的概率.
的值,求恰有一个数据使得函数没有零点的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com