
【题目】已知不共线向量![]() ,
,![]() 满足|
满足|![]() |=3,|
|=3,|![]() |=2,(2
|=2,(2![]() 3
3![]() )(2
)(2![]() )=20.
)=20.
(1)求![]()
![]() ;
;
(2)是否存在实数λ,使λ![]() 与
与![]() 2
2![]() 共线?
共线?
(3)若(k![]() 2
2![]() )⊥(
)⊥(![]() ),求实数k的值.
),求实数k的值.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
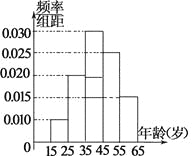
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 |
| 5 | 0.5 |
第2组 |
|
| 0.9 |
第3组 |
| 27 |
|
第4组 |
|
| 0.36 |
第5组 |
| 3 |
|
(Ⅰ) 分别求出![]() 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域存在实数
,若在定义域存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() (
(![]()
![]() ),试判断
),试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若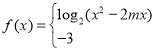
![]() 为其定义域上的“局部奇函数”,求实数
为其定义域上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,对于定义域内的任意实数
,对于定义域内的任意实数![]() ,有
,有![]() 成立,且
成立,且![]() 时,
时,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(3)已知![]() (实数
(实数![]() ),求实数
),求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 直角坐标方程;
直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图表示一位骑自行车者和一位骑摩托车者在相距![]() 的两城镇间旅行的函数图象,由图,可知骑自行车者用了
的两城镇间旅行的函数图象,由图,可知骑自行车者用了![]() ,沿途休息了
,沿途休息了![]() ,骑摩托车者用了
,骑摩托车者用了![]() ,根据这个图象,提出关于这两个旅行者的如下信息:
,根据这个图象,提出关于这两个旅行者的如下信息:

①骑自行车者比骑摩托车者早出发![]() ,晚到
,晚到![]() ;
;
②骑自行车者是变速运动,骑摩托者是匀速运动;
③骑摩托车者在出发了![]() 后,追上了骑自行车者.
后,追上了骑自行车者.
其中正确信息的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上周某校高三年级学生参加了数学测试,年级组织任课教师对这次考试进行成绩分析现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组;第二组;……;第六组,并据此绘制了如图所示的频率分布直方图.
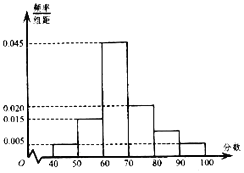
(1)估计这次月考数学成绩的平均分和众数;
(2)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com