
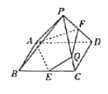
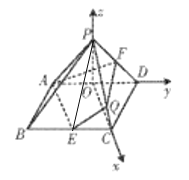
【题目】如图,在底面为菱形的四棱锥P-ABCD中,平面![]() 平面ABCD,
平面ABCD,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,点E,F分别为BC,PD的中点,直线PC与平面AEF交于点Q.
,点E,F分别为BC,PD的中点,直线PC与平面AEF交于点Q.
(1)若平面![]() 平面
平面![]() ,求证:
,求证:![]() .
.
(2)求直线AQ与平面PCD所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据线面平行的判定定理证得![]() 平面
平面![]() ,然后根据线面平行的性质定理证得
,然后根据线面平行的性质定理证得![]() .(2)先根据
.(2)先根据![]() 四点共面,结合向量的线性运算,求得
四点共面,结合向量的线性运算,求得![]() ,也即求得
,也即求得![]() 位置.建立空间直角坐标系,利用直线
位置.建立空间直角坐标系,利用直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,求得线面角的正弦值.
的法向量,求得线面角的正弦值.
(1)证明:因为![]() ,
,![]() 平面PC,
平面PC,![]() 平面PCD,
平面PCD,
所以![]() 平面PCD.又因为
平面PCD.又因为![]() 平面PAB,平面
平面PAB,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解:连接PE.
因为![]() ,
,
所以![]() ,
,
则![]()
设![]() ,则
,则![]() .
.
因为A,E,Q,F四点共面,
所以![]() ,解得
,解得![]() ,则
,则![]() .
.
取AD的中点O,连接OC,OP,由题意可得OC,OD,OP两两垂直
如图,建立空间直角坐标系,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面PCD的一个法向量为![]() ,
,
则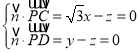 ,令
,令![]() ,得
,得![]() ,即
,即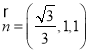 ,
,
所以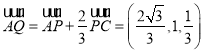 ,
,
所以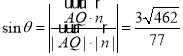 .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】在一次运动会上,某单位派出了由6名主力队员和5名替补队员组成的代表队参加比赛.
(1)如果随机抽派5名队员上场比赛,将主力队员参加比赛的人数记为![]() ,求随机变量
,求随机变量![]() 的数学期望;
的数学期望;
(2)若主力队员中有2名队员在练习比赛中受轻伤,不宜同时上场;替补队员中有2名队员身材相对矮小,也不宜同时上场,那么为了场上参加比赛的5名队员中至少有3名主力队员,教练员有多少种组队方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 经过曲线
经过曲线![]() 的焦点
的焦点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称;
轴对称;
②若函数![]() ,则
,则![]() ,都有
,都有![]() ;
;
③若函数![]() ,
,![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ;
;
④若函数![]()
![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]() .
.
其中真命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com