
河北省邢台一中06―07学年上学期第一次月考高三数学试题(文科)
命题人:李振生 考试时间:120分钟
第Ⅰ卷(选择题共60分)
一、选择题:(每小题5分,共60分)
(1) 已知集合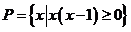 ,
,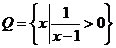 ,则
,则 等于
等于
(A) 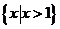 (B)
(B) 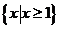 (C)
(C) 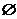 (D)
(D)  或
或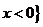
(2) 已知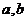 为实数,集合
为实数,集合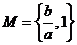 ,
,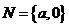 ,
,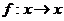 表示把
表示把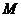 中的元素
中的元素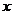 映射到集合
映射到集合 中仍为
中仍为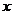 ,则
,则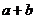 等于
等于
(A) 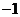 (B)
(B) 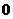 (C)
(C) 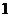 (D)
(D)

(3) 函数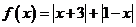 的最小值是
的最小值是
(A) 2 (B) 3 (C) 4 (D) 5
(4) 不等式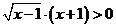 的解集是
的解集是
(A) 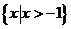 (B)
(B)  (C)
(C) 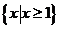 (D)
(D) 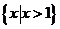
(5) 已知集合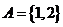 ,集合
,集合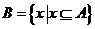 ,则以下选项正确的是
,则以下选项正确的是
(A) 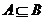 (B)
(B) 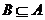 (C)
(C) 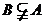 (D)
(D) 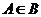
(6) 若函数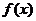 是定义在
是定义在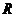 上的偶函数,在
上的偶函数,在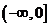 上是减函数,且
上是减函数,且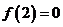 ,则使得
,则使得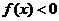 的
的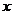 的取值范围是
的取值范围是
(A) 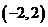 (B)
(B) 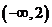 (C)
(C) 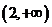 (D)
(D) 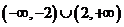
(7) 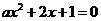 至少有一个负的实根的充要条件是
至少有一个负的实根的充要条件是
(A) 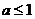 (B)
(B) 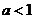 (C)
(C) 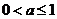 (D)
(D) 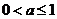 或
或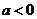
(8) 能成为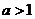 的必要而不充分条件的是
的必要而不充分条件的是
① 函数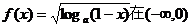 上是减函数;
上是减函数;
② 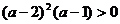 ;
;
③ 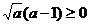 ;
;
④ 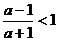 ;
;
(A) ①② (B) ③④ (C) ②③ (D) ②④
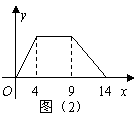
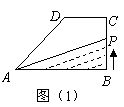
(9) 直角梯形ABCD如图(1)所示,动点P从B点出发,由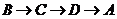 沿边运动,设点P运动的路程为
沿边运动,设点P运动的路程为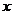 ,
,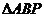 的面积为
的面积为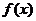 .如果函数
.如果函数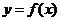 的图象如图(2)所示,则
的图象如图(2)所示,则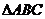 的面积为
的面积为
 |
|||
 |
|||
(A) 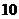 (B)
(B)
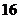 (C)
(C)
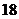 (D)
(D)
(10) 设函数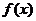 是定义在
是定义在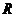 上,周期为
上,周期为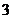 的奇函数若
的奇函数若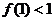 ,
,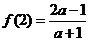 ,则实数
,则实数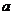 的取值范围是
的取值范围是
(A) 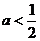 且
且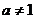 (B)
(B)
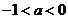
(C) 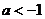 或
或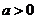 (D)
(D) 
(11) 如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好点”.在下面的五个点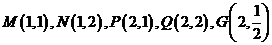 中,“好点”的个数为
中,“好点”的个数为
(A) 0个 (B) 1个 (C) 2个 (D) 3个
(12)
如果函数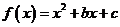 对任意实数
对任意实数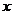 ,都有
,都有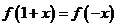 ,那么
,那么
(A) 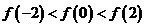 (B)
(B)
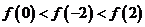
(C) 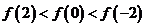 (D)
(D)
第Ⅱ卷(非选择题共90分)
题号
二
17
18
19
20
21
22
总分
分数
二、填空题:(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
(13)
已知函数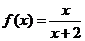 ,则
,则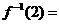 .
.
(14) 函数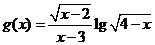 的定义域是
.
的定义域是
.
(15) 函数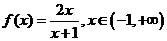 的图象与其反函数的图象的交点坐标是
.
的图象与其反函数的图象的交点坐标是
.
(16) 为了保证信息安全传输,有一种称为秘密密钥密码系统,其加密、解密原理如下图:
明文 ―→ 密文 ―→ 密文 ―→ 明文
现在加密密钥为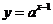
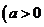 且
且 ,如上所示,“3”通过加密后得到密文“4”,再发送,接收方通过解密密钥解密后得到明文“3”.问:接收方接到密文“32”,则解密后得到明文为
.
,如上所示,“3”通过加密后得到密文“4”,再发送,接收方通过解密密钥解密后得到明文“3”.问:接收方接到密文“32”,则解密后得到明文为
.
(17) (本小题满分12分)
三、解答题:(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤)
已知函数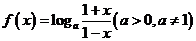 .
.
(Ⅰ)求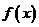 的定义域;
的定义域;
(Ⅱ)当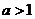 时,求使
时,求使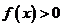 的
的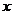 取值范围.
取值范围.
(18) (本小题满分12分)
已知函数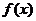
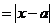 ,
,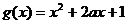 (
(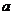 为正常数),且函数
为正常数),且函数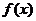 与
与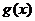 的图象在
的图象在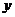 轴上的截距相等.
轴上的截距相等.
(Ⅰ)求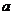 的值;
的值;
(Ⅱ)求函数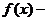
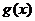 的单调递增区间.
的单调递增区间.
(19) (本小题满分12分)
设函数 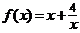 .
.
(Ⅰ)求函数在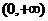 上的单调增区间,并证明之;
上的单调增区间,并证明之;
(Ⅱ)若函数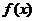 在
在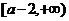 上递增,求实数
上递增,求实数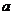 的取值范围.
的取值范围.
(20) (本小题满分12分)
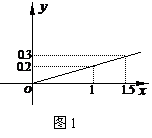 某投资公司计划投资
某投资公司计划投资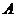 、
、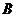 两种金融产品,根据市场调查与预测,
两种金融产品,根据市场调查与预测,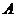 产品的利润与投资量成正比例,其关系如图1,
产品的利润与投资量成正比例,其关系如图1,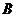 产品的利润与投资量的算术平方根成正比例,其关系如图2,(注:利润与投资量单位:万元)
产品的利润与投资量的算术平方根成正比例,其关系如图2,(注:利润与投资量单位:万元)
(Ⅰ)分别将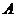 、
、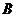 两产品的利润表示为投资量的函数
两产品的利润表示为投资量的函数
关系式;
(Ⅱ)该公司已有10万元资金,并全部投入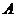 、
、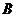 两
两
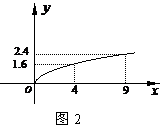 种产品中,问:怎样分配这10万元投资,才能使公司获
种产品中,问:怎样分配这10万元投资,才能使公司获
得最大利润?其最大利润为多少万元?
(21) (本小题满分12分)
已知点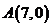 在曲线
在曲线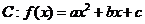 (其中
(其中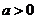 )上,且曲线
)上,且曲线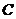 在点
在点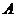 处的切线与直线
处的切线与直线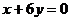 垂直,又当
垂直,又当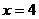 时,函数
时,函数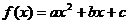 有最小值.
有最小值.
(Ⅰ)求实数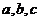 的值;
的值;
(Ⅱ)设函数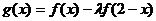 的最大值为
的最大值为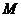 ,求正整数
,求正整数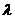 的值,使得
的值,使得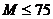 成立.
成立.
(22) (本小题满分14分)
对于函数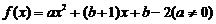 ,若存在实数
,若存在实数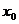 ,使
,使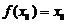 成立,则称
成立,则称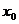 为
为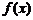 的不动点.
的不动点.
(Ⅰ)当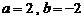 时,求
时,求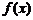 的不动点;
的不动点;
(Ⅱ)若对于任何实数 ,函数
,函数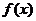 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数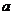 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若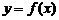 的图象上
的图象上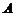 、
、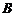 两点的横坐标是函数
两点的横坐标是函数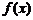 的不动点,且直线
的不动点,且直线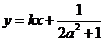 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.
邢台一中2006―2007学年上学期第一次月考
一、选择题:(每小题5分,共60分)
A C C D D A A B B C C D
注:选择题第⑺题选自课本43页第6题.
二、填空题:(每小题4分,共16分)
(13)  ; (14)
; (14)  ; (15)
; (15)  ; (16) 6.
; (16) 6.
三、解答题:(本大题共6小题,共74分)
(17)
解:(Ⅰ)由对数函数的定义域知 .
………………2分
.
………………2分
解这个分式不等式,得 .
………………4分
.
………………4分
故函数 的定义域为
的定义域为 .
………………5分
.
………………5分
(Ⅱ) ,
………………8分
,
………………8分
因为 ,所以由对数函数的单调性知
,所以由对数函数的单调性知 .
………………9分
.
………………9分
又由(Ⅰ)知 ,解这个分式不等式,得
,解这个分式不等式,得 . ………………11分
. ………………11分
故对于 ,当
,当 ,
, ………………12分
………………12分
(18)
解:(Ⅰ)由题意 ,
, =1又a>0,所以a=1.………………4分
=1又a>0,所以a=1.………………4分
(Ⅱ) -
- =
= ,
………………6分
,
………………6分
当 时,
时, -
- =
= ,无递增区间; ………………8分
,无递增区间; ………………8分
当x<1时, -
- =
= ,它的递增区间是
,它的递增区间是 .……11分
.……11分
综上知: -
- 的单调递增区间是
的单调递增区间是 . ……………12分
. ……………12分
(19)证明:(Ⅰ) 函数在 上的单调增区间为
上的单调增区间为 .
.
(证明方法可用定义法或导数法) ……………8分
(Ⅱ) 
 ,所以
,所以 ,解得
,解得 . ……………12分
. ……………12分
(20)
解:(Ⅰ)设投资为 万元,
万元, 产品的利润为
产品的利润为 万元,
万元, 产品的利润为
产品的利润为 万元.由题意设
万元.由题意设 ,
, .
.
由图可知 ,
, . ………………2分
. ………………2分
又 ,
, .
………………4分
.
………………4分
从而 ,
, .
………………5分(Ⅱ)设
.
………………5分(Ⅱ)设 产品投入
产品投入 万元,则
万元,则 产品投入
产品投入 万元,设企业利润为
万元,设企业利润为 万元.
万元.

 ,
………………7分
,
………………7分
令 ,则
,则

 .
.
当 时,
时, ,此时
,此时 .
………………11分
.
………………11分
答:当 产品投入6万元,则
产品投入6万元,则 产品投入4万元时,该企业获得最大利润,利润为2.8万元.
………………12分
产品投入4万元时,该企业获得最大利润,利润为2.8万元.
………………12分
(21)解:(Ⅰ) ……1分
……1分
根据题意, …………4分
…………4分
解得 . …………6分
. …………6分
(Ⅱ)因为 …………7分
…………7分
(i) 时,函数
时,函数 无最大值,
无最大值,
不合题意,舍去. …………9分
(ii) 时,根据题意得
时,根据题意得

解之得 …………11分
…………11分
 为正整数,
为正整数,  =3或4. …………12分
=3或4. …………12分
(22) 解: ,
,
(Ⅰ)当 时,
时, ………………2分
………………2分
设 为其不动点,即
为其不动点,即 则
则
 即
即 的不动点是
的不动点是 . ……………4分
. ……………4分
(Ⅱ)由 得:
得: . 由已知,此方程有相异二实根,
. 由已知,此方程有相异二实根,
 恒成立,即
恒成立,即 即
即 对任意
对任意 恒成立.
恒成立.
 ………………8分(Ⅲ)设
………………8分(Ⅲ)设 ,
,
直线 是线段AB的垂直平分线, ∴
是线段AB的垂直平分线, ∴  …………10分
…………10分
记AB的中点 由(Ⅱ)知
由(Ⅱ)知
 ……………………12分
……………………12分
化简得:
(当 时,等号成立).
时,等号成立).
即 ……………………14分
……………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com