|
试题详情
试题详情
已知数列 为正常数,且 为正常数,且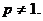 试题详情
(I)求数列 的通项公式; 的通项公式; 试题详情
(II)设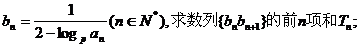 试题详情
(III)是否存在正整数M,使得 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。 试题详情
试题详情
试题详情
(I)求 的值; 的值; 试题详情
(II)设 的图象上两点, 的图象上两点, 试题详情
试题详情
如图,曲线 的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为 的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为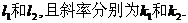 试题详情
(I) 无关?若是,给出证明;若否,给以说明; 无关?若是,给出证明;若否,给以说明; 试题详情
 (II)若 (II)若 取得最小值9时,求曲线C1与抛物线C2的方程。 取得最小值9时,求曲线C1与抛物线C2的方程。
试题详情
一、选择题:本大题共12小题,每小题5分,共60分。 BBDD CABC BCDB 二、填空题:本大题共4小 题,每小题4分,共16分。 13.8500 14. 15. 16.①③ 三、解答题:本大题共6小题,共74分。 17.解:(I)依题意, 由正弦定理及 3分 3分  6分
6分 (II)由 由 (舍去负值) 8分 (舍去负值) 8分 从而, 9分 9分 由余弦定理,得 代入数值,得 解得 12分 12分 18.解:(I)随意抽取4件产品进行检查是随机事件,而第一天有9件正品, 第一天通过检查的概率为错误!嵌入对象无效。 2分 第二天通过检查的概率为 错误!嵌入对象无效。 4分 因为第一天、第二天检查是否通过是相互独立的, 所以两天全部通过检查的概率为错误!嵌入对象无效。 6分 (II)记所得奖金为 元,则 元,则 的取值为-300,300,900 7分 的取值为-300,300,900 7分    10分 10分  (元) 12分 (元) 12分 19.解:(I)如图,以AB,AC,AA1分别为 轴,建立空间直角坐标系 轴,建立空间直角坐标系 则 2分 2分 从而  
所以 3分 3分 (II)平面ABC的一个法向量为 则  (※) 5分 (※) 5分 而 由(※)式,当 6分 6分 (III)平面ABC的一个法向量为 设平面PMN的一个法向量为 由(I)得 由 7分 7分 解得 9分 9分  平面PMN与平面ABC所成的二面角为45°, 平面PMN与平面ABC所成的二面角为45°,  解得 11分 11分 故点P在B1A1的延长线上,且 12分 12分 20.(本小题满发12分) 解:(I)由题设知 1分 1分 同时 两式作差得 所以 可见,数列  4分 4分 (II) 5分 5分     7分 7分 (III)  9分 9分 ①当 解得 符合题意,此时不存在符合题意的M。 10分 符合题意,此时不存在符合题意的M。 10分 ②当 解得 此时存在的符合题意的M=8。 11分 此时存在的符合题意的M=8。 11分 综上所述,当 时,存在M=8符合题意 12分 时,存在M=8符合题意 12分 21.解:(I)因为 所以 因为 上是增函数。 上是增函数。 所以 上恒成立 1分 上恒成立 1分 当 而 上的最小值是-1。 上的最小值是-1。 于是 (※) (※) 可见 从而由(※)式即得 ① 4分 ① 4分 同时, 由 解得 ②, ②, 或 由①②得  此时, 即为所求 6分 即为所求 6分 注:没有提到(验证) 时, 时, 不扣分。 不扣分。 (II)由(I), 于是 7分 7分 以下证明 (☆) (☆) (☆)等价于 8分 8分 构造函数 则 时, 时,  上为增函数。 上为增函数。 因此当 即 从而 得到证明。 11分 得到证明。 11分 同理可证 12分 12分 注:没有“综上”等字眼的结论,扣1分。  22.(I)设 22.(I)设 得 得
 即 2分 2分 由 则 所以 (※) 4分 (※) 4分 又因为 则 代入(※)式得  可见, 无关。 6分 无关。 6分 (II)如图,设 由(I)知 7分 7分 又 所以 8分 8分 将点A的坐标代入曲线C1的方程得 则 10分 10分 当且仅当“=”成立时,有 11分 11分 解得 14分 14分
| 

 为 ( )
为 ( )
 面A1B1C1,正视图是边长为2的正方形,该三棱柱的侧视图面积为 ( )
面A1B1C1,正视图是边长为2的正方形,该三棱柱的侧视图面积为 ( )