
2009-2010学年度招远市第一学期初四第一学段测评
数学试卷
说明:本试题满分120分,其中试题共115分,书写质量3分,卷面安排2分。
一、选择题(每小题2分,满分30分)
1.函数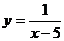 中,自变量
中,自变量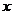 的取值范围是
的取值范围是
A. 的实数 B.
的实数 B.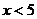 的实数 C.
的实数 C.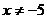 的实数 D.
的实数 D.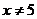 的实数
的实数
2.在Rt△ABC中,∠C=90°,下列各式中正确的是
A.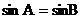 B.
B.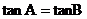 C.
C.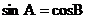 D.
D.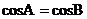
3.抛物线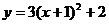 的顶点坐标是
的顶点坐标是
A.(1,2) B.(1,-2) C.(-1,-2) D.(-1,2)
4.在△ABC中,若∠A、∠B都是锐角,且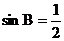 ,
,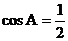 ,则△ABC的形状是
,则△ABC的形状是
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
5.若抛物线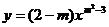 的开口向上,则
的开口向上,则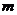 的值为
的值为
A.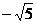 B.
B. C.
C. D.0
D.0
6.若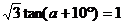 ,则锐角
,则锐角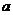 的度数是
的度数是
A.20° B.30° C.40° D.50°
7.抛物线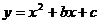 上有两点(3,-8)和(-5,-8),则此抛物线的对称轴是
上有两点(3,-8)和(-5,-8),则此抛物线的对称轴是
A.直线 B.直线
B.直线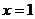 C.直线
C.直线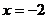 D.直线
D.直线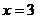
8.下图是河堤的横断面,若堤高BC=
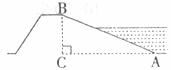
A.1┱2 B.1┱
9.二次函数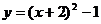 的图像可以由二次函数
的图像可以由二次函数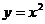 的图像平移而得到,下列平移正确的是
的图像平移而得到,下列平移正确的是
A.先向右平移2个单位,再向下平移1个单位
B.先向右平移2个单位,再向上平移1个单位
C.先向左平移2个单位,再向上平移1个单位
D.先向左平移2个单位,再向下平移1个单位
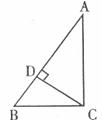
10.如下图,在△ABC中,∠ACB=90°,CD⊥AB于点D。若AC=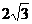 ,AB=
,AB=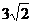 ,则
,则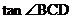 的值为
的值为
A.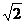 B.
B. C.
C.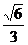 D.
D.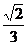
11.若抛物线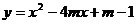 经过原点O,与
经过原点O,与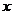 轴的另一个交点为A,抛物线的顶点为B,则△OAB的面积为
轴的另一个交点为A,抛物线的顶点为B,则△OAB的面积为
A.16 B.8 C.4 D.2
12.Rt△ABC中,∠C=90°,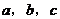 分别是∠A,∠B,∠C的对边,则
分别是∠A,∠B,∠C的对边,则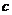 等于
等于
A.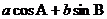 B.
B.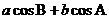
C.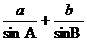 D.
D.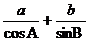
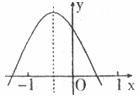
13.二次函数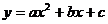 的图像如下图所示,则下列判断不正确的是
的图像如下图所示,则下列判断不正确的是
A.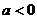 B.
B.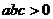 C.
C.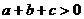 D.
D.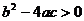
14.如下图,小亮站在楼顶观测对面笔直的旗杆AB,已知观测点C到旗杆的距离为10米,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45°,则旗杆的高度为
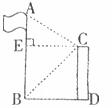
A.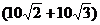 米 B.
米 B.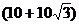 米
米
C.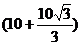 米 D.
米 D.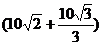 米
米
15.一个长方形的周长是8cm,一边长是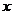 cm,则这个长方形的面积
cm,则这个长方形的面积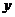 与边长
与边长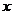 的函数关系用图像表示为
的函数关系用图像表示为
二、填空题(每小题3分,满分30分)
16.请写出一个图像开口向上,且顶点在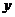 轴的负半轴上的二次函数的表达式___________。
轴的负半轴上的二次函数的表达式___________。
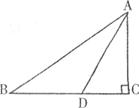
17.如下图,△ABC中,∠C=90°,AD是BC边的中线,∠ABC=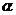 ,∠ADC=
,∠ADC=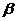 ,则
,则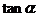 与
与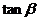 之间的关系是___________。
之间的关系是___________。
18.若抛物线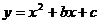 的顶点是(1,-2),则
的顶点是(1,-2),则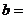 ___________,
___________,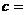 ___________。
___________。
19.在△ABC中,∠C=90°, ,AC=
,AC=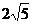 ,则AB=___________。
,则AB=___________。
20.二次函数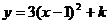 的图像上有A(
的图像上有A(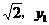 ,),B(2,
,),B(2,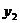 ),C(
),C( )三个点
)三个点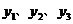 ,则的大小关系是___________。
,则的大小关系是___________。
21.若抛物线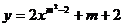 的顶点在
的顶点在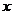 轴上方,则
轴上方,则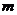 的值是___________。
的值是___________。
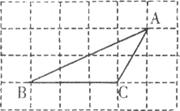
22.如下图,△ABC的顶点都是正方形网格中的格点,则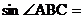 ___________。
___________。
23.生产季节性产品的企业,当它的产品无利润时就会及时停产。现有一生产季节性产品的企业,其一年中获得的利润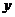 (万元)和月份
(万元)和月份 之间的函数表达式为
之间的函数表达式为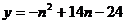 ,则该企业一年中应停产的月份是___________。
,则该企业一年中应停产的月份是___________。
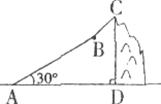
24.如下图,一旅游者由山脚A滑坡角为30°的山坡AB行走800m,到达一个景点B,再由B沿山坡BC行走300m,到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD等于___________(结果用根号表示)。
25.小明同学利用计算机设计了一个计算程序,输入和输出的数据如下表:
输入
……
1
2
3
4
5
……
输出
……
2
5
10
17
26
……
若输入的数据是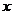 时,输出的数据是
时,输出的数据是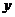 ,且
,且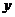 是
是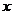 的二次函数,则
的二次函数,则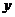 与
与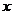 的函数表达式为___________。
的函数表达式为___________。
三、解答题(每小题8分,满分24分)
26.计算:
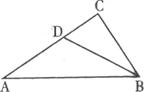
27.如下图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,若BC=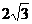 ,求△ABC的周长。
,求△ABC的周长。
28.已知抛物线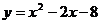 。
。
(1)求证:此抛物线与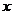 轴有两个交点;
轴有两个交点;
(2)若该抛物线与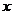 轴的两个交点分别为A,B(A在B的左边),且它的顶点为P,求△ABP的面积。
轴的两个交点分别为A,B(A在B的左边),且它的顶点为P,求△ABP的面积。
四、实际应用题(每小题10分,满分20分)
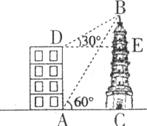
29.如下图,小芳想测量塔BC的高度。她在一楼底A处测得塔顶B的仰角为60°,爬到楼顶D处测得大楼AD的高度为18米,同时测得塔顶B的仰角为30°,求塔BC的高度。
30.某企业进行市场调查发现:
信息一:如果单独投资甲种产品,则所获利润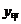 (万元)与投资金额
(万元)与投资金额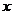 (万元)之间存在正比例函数关系:
(万元)之间存在正比例函数关系: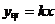 ,且当投资5万元时,可获利润2万元。
,且当投资5万元时,可获利润2万元。
信息二:如果单独投资乙种产品,则所获利润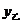 (万元)与投资金额
(万元)与投资金额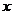 (万元)之间存在二次函数关系:
(万元)之间存在二次函数关系: ,且当投资2万元时,可获利润2.4万元;当投资4万元时,可获利润3.2万元。
,且当投资2万元时,可获利润2.4万元;当投资4万元时,可获利润3.2万元。
(1)请你分别求出上述正比例函数表达式和二次函数表达式;
(2)如果企业同时对甲、乙两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案投资可获得的最大利润。
五、探索题(满分11分)
31.已知抛物线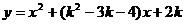 与
与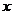 轴从左至右交于A、B两点,且这两点关于原点对称。
轴从左至右交于A、B两点,且这两点关于原点对称。
(1)求 的值;
的值;
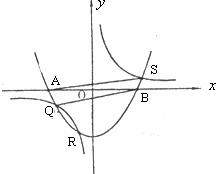
(2)在(1)的条件下,若反比例函数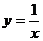 的图像与抛物线
的图像与抛物线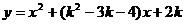 从左至右交于Q、R、S三点,且Q的坐标(-1,-1),R的坐标(
从左至右交于Q、R、S三点,且Q的坐标(-1,-1),R的坐标(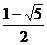 ,
,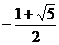 ),S的坐标(
),S的坐标(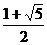 ,
,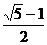 ),求四边形AQBS的面积;
),求四边形AQBS的面积;
(3)在(1)、(2)条件下,在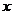 轴下方抛物线
轴下方抛物线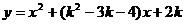 上是否存在点P,使
上是否存在点P,使 ?若存在求出P点坐标,若不存在,请说明理由。
?若存在求出P点坐标,若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com