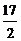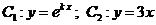|
试题详情
试题详情
试题详情
6.由直线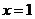 ,x=2,曲线 ,x=2,曲线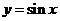 及x轴所围图形的面积为 及x轴所围图形的面积为
试题详情
A. B. B.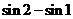 试题详情
C. D. D.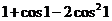 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
11.已知定点A(2, 1), 动点P (x, y) 满足: 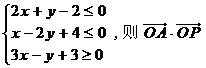 最小值是 最小值是 试题详情
试题详情
12.如图,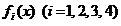 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的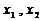 和任意 和任意 恒成立”的只有 恒成立”的只有 A.(1).(3) B.(1)
C.(2) D.(3).(4) 试题详情
试题详情
13.设 100 件产品中有 70 件一等品,25 件二等品,规定一.二等品为合格品.从中任取1件, 已知取得的是合格品,则它是一等品的概率为
14.若x>1,不等式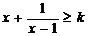 恒成立,则实数k的取值范围是 恒成立,则实数k的取值范围是
试题详情
试题详情
16.为了分析广告费用x与销售额y之间的关系,抽取了五家餐厅,得到如下数据: 广告费用
(千元) 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
53.0
现要使销售额达到9万元,则需要广告费用为
(保留两位有效数字) 试题详情
三.解答题:解答应写出文字说明,证明过程或演算步骤.
试题详情
试题详情
试题详情
(Ⅰ)求证: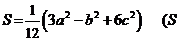 是△ 是△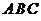 的面积); 的面积); 试题详情
试题详情
试题详情
掷两枚骰子,它们的各面点数都分别为1,2,2,3,3,3,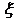 为两枚骰子的点数之和. 为两枚骰子的点数之和. 试题详情
(Ⅰ)写出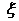 的分布列. 的分布列. (Ⅱ)求: 掷出的两枚骰子的点数相同的概率。 试题详情
试题详情
试题详情
试题详情
(Ⅰ)求直线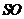 与底面 与底面 所成角的正切值; 所成角的正切值; 试题详情
(Ⅱ)设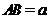 ,求此四棱锥过点 ,求此四棱锥过点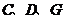 的截面面积. 的截面面积. 试题详情
试题详情
已知函数 若数列{a n}满足: 若数列{a n}满足: 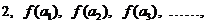 试题详情
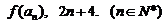 成等差数列. 成等差数列. (Ⅰ)求{a n}的通项a n ; 试题详情
(Ⅱ)设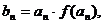 若{b n}的前n项和是S n,且 若{b n}的前n项和是S n,且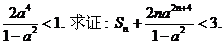 试题详情
试题详情
试题详情
(Ⅰ)设直线 的斜率为1,求 的斜率为1,求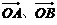 夹角的余弦值; 夹角的余弦值; 试题详情
试题详情
试题详情
已知函数 试题详情
试题详情
试题详情
(Ⅲ)讨论方程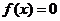 解的个数,并说明理由. 解的个数,并说明理由. 试题详情
一.选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C B C A D C B A D D A 二.13. 14. 14. 15. 15. 16. 16. (万元) (万元) 三.17.(I) 由 代入
 得: 得:
整理得: (5分)
(5分) (II)由  由余弦定理得: 由余弦定理得: ∴  -----------------------------
(9分)
-----------------------------
(9分)
  又
 ------ (12分) ------ (12分) 18.(Ⅰ)  的分布列. 的分布列. 
2 3 4 5 6 p   


- --------- ------ (4分) (Ⅱ)设掷出的两枚骰子的点数同是 为事件 为事件 同掷出1的概率 ,同掷出2的概率 ,同掷出2的概率 ,同掷出3的概率 ,同掷出3的概率 所以,掷出的两枚骰子的点数相同的概率为P=   (8分) (8分) (Ⅲ)   时) 时)
 2 3 4 5 6  3
6
6
6
6 p 




 = =
 时) 时)
 2 3 4 5 6  2
5
8
8
8 p 




 = =
 时) 时)
 2 3 4 5 6  1
4
7 10
10 p 




 = =
 时, 时,  最大为 最大为 (12分)
(12分)
19.(Ⅰ)    两两相互垂直, 连结 两两相互垂直, 连结 并延长交 并延长交 于F. 于F.
  同理可得     ------------ (6分) ------------ (6分) (Ⅱ) 是 是 的重心 的重心 F是SB的中点   梯形的高  --- (12分) --- (12分) 【注】可以用空间向量的方法 20.设2,f (a1),
f (a2),
f (a3),
…,f (an), 2n+4的公差为d,则2n+4=2+(n+2-1)d  d=2, d=2,   ……………………(4分) ……………………(4分)
(2) , ,  
 --------------------
(8分) --------------------
(8分) 
 
21.(Ⅰ)∵直线 的斜率为1,抛物线 的斜率为1,抛物线 的焦点 的焦点 ∴直线 的方程为 的方程为 由 设 则 又 
 故  夹角的余弦值为 夹角的余弦值为 ----------------- (6分) ----------------- (6分) (Ⅱ)由 即得: 由  从而得直线 的方程为 的方程为 ∴ 在 在 轴上截距为 轴上截距为 或 或
∵ 是 是 的减函数 的减函数 ∴  从而得 从而得 故 在 在 轴上截距的范围是 轴上截距的范围是  ------------ (12分) ------------ (12分) 22.(Ⅰ)   在直线 在直线 上, 上, ?????????????? (4分) (Ⅱ)  在 在 上是增函数, 上是增函数, 在 在 上恒成立 上恒成立 所以得  ??????????????? (8分) ??????????????? (8分) (Ⅲ) 的定义域是 的定义域是 , , ①当 时, 时, 在 在 上单增,且 上单增,且 , , 无解; 无解; ②当 时, 时, 在 在 上是增函数,且 上是增函数,且 , ,  有唯一解; 有唯一解;
③当 时, 时, 那么在 上 上 单减,在 单减,在 上 上 单增, 单增, 而  时, 时, 无解; 无解;  时, 时, 有唯一解 有唯一解  ; ;  时, 时, 那么在 上, 上, 有唯一解 有唯一解 而在 上,设 上,设  
即得在 上, 上, 有唯一解. 有唯一解. 综合①②③得: 时, 时, 有唯一解; 有唯一解;   时, 时, 无解; 无解;  时, 时, 有且只有二解. 有且只有二解. ?????????????? (14分)
| 
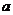 是实数,且
是实数,且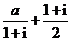 是纯虚数,则
是纯虚数,则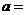
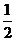 B.
B.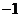 C.
C.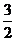 D.
D.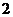
 所有的有理数都是实数,命题
所有的有理数都是实数,命题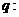 正数的对数都是负数,则下列命题中为真的是
正数的对数都是负数,则下列命题中为真的是 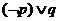 B.
B.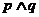 C.
C.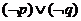 D.
D.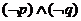
 3.若
3.若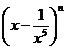 的展开式中不含有常数项,那么
的展开式中不含有常数项,那么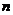 的取值可以是
的取值可以是
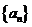 的公比q=2,前n项和为Sn,则
的公比q=2,前n项和为Sn,则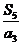 =
=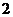 B.
B.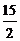 C.
C.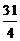 D.
D.