
1.已知 ,全集I=R,则A∩ 为 ( )
,全集I=R,则A∩ 为 ( )
A. B.
B.
C. D.
D.
2.函数 的最小值为 ( )
的最小值为 ( )
A.-1 B.- -1 C.-
-1 C.- D.0
D.0
3.已知函数 的取值范围是 ( )
的取值范围是 ( )
A.(-∞,0) B.(-1,1) C.(1,+∞) D.(-∞,-1)
4.函数 的图象与函数
的图象与函数 的图象关于 (
)
的图象关于 (
)
A.直线y= x对称 B.直线y=x-1对称
C.直线y= x
+1对称 D.直线y=-x+1对称
5.一个球的内接正四棱柱的侧面积与上下两底面积的和之比为4:1,且该正四棱柱的体积为
 ,则这个球的表面积为 ( )
,则这个球的表面积为 ( )
A.12 B.12π C. D.12
D.12
6.甲袋中装有3个白球5个黑球,乙袋中装有4个白球6个黑球,现从甲袋中随机取出一个球放入乙袋
中,充分惨混后再从乙袋中随机取出一个球放回甲袋,则甲袋中白球没有减少的概率为( )
A. B.
B. C.
C. D.
D.
7.各项均不为零的等差数列{an}中,若 ,则S2006-2006=( )
,则S2006-2006=( )
A.0 B.4012 C.-2006 D.2006
8.已知D为△ABC的边BC的中点,在△ABC所在平面内有一点P,满足 ,设
,设 ,则
,则 的值为 ( )
的值为 ( )
A.1 B.2 C. D.
D.
9.已知平面 ,定点P
,定点P 之间的距离为8,则在
之间的距离为8,则在 内到P点的距离为10点的轨迹是 ( )
内到P点的距离为10点的轨迹是 ( )
A.一个圆 B.两条直线 C.四个点 D.两个点
1,3,5 A. B. B. C. C. D. D. 11.若函数 ,则函数 ,则函数 的图象与函数 的图象与函数 的图象的交点个数为 ( ) 的图象的交点个数为 ( ) A.16 B.18 C.20 D.无数个 12.某校需要在5名男生和5名女生中选出4人参加一项文化交流活动,由于工作需要,男生甲与男生乙至少有一人参加活动,女生丙必须参加活动,则不同的选人方式有( ) A.56种 B.49种 C.42种 D.14种 二、填空题(本大题共4小题,每小题5分,共20分. 请把答案填在答题卡上) 13.若 = =
试题详情
14.已知两圆 相交于A,B两点,则直线AB的方程是 相交于A,B两点,则直线AB的方程是 试题详情
15.在棱长为1的正四面体ABCD中,E、F分别是BC,AD的中点,则 = = 试题详情
16.已知 的最小值为 的最小值为 试题详情
三、解答题(本大题共6小题,共70分,请把解答和推理过程写在答题卡上)
试题详情
已知A、B、C是△ABC的三个内角,向量 (1)求角A; 试题详情
(2)若 ,求tanB. ,求tanB. 试题详情
18.(本小题12分) 袋中有红球3个、蓝球2个、黄球1个,共6个球. (1)若每次任取1球,取出的球不放回袋中,求第3次取球才得到红球的概率; (2)若每次任取1球,取出的球放回袋中,求第3次取球才得到红球的概率. 试题详情
试题详情
如图,在底面是菱形的四棱锥P―ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ,点E在PD上,且PE : ED=2 : 1. ,点E在PD上,且PE : ED=2 : 1. 试题详情
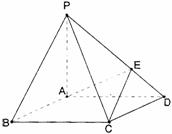
(2)求以AC为棱EAC与DAC为面的二面角θ的大小.
试题详情
试题详情
设数列 前n项和为Sn,且 前n项和为Sn,且 试题详情
(Ⅰ)求 的通项公式; 的通项公式; (Ⅱ)若数列{bn}满足b1=1且bn+1=bn+an(n≥1),求数列{bn}的通项公式 试题详情
试题详情
已知双曲线的两条渐近线方程为直线 ,其焦点在x轴上,实轴长为2. ,其焦点在x轴上,实轴长为2. (Ⅰ)求双曲线的方程; 试题详情
(Ⅱ)设直线 与双曲线相切于点M且与右准线交于N,F为右焦点,求证:∠MFN为直 与双曲线相切于点M且与右准线交于N,F为右焦点,求证:∠MFN为直 角.
试题详情
试题详情
已知函数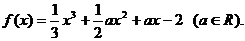 试题详情
(1)若函数 上为单调函数,求实数a的取值范围; 上为单调函数,求实数a的取值范围; 试题详情
(2)设 是函数 是函数 的两个极值点,若直线AB的斜率不小 的两个极值点,若直线AB的斜率不小 试题详情
于 ,求实数a的取值范围. ,求实数a的取值范围. 云南省昆明一中2008届高三年级10月检测 数学试题(文科) 试题详情
一、选择题 1.C 2.A
3.D 4.C 5.B
6.C 7.D 8.B
9.A 10.C 11.B 12.B
1,3,5 13. 14. 14. =0 15.- =0 15.- 16.3 16.3 三、解答题 17.解:(1)∵ ……2分 ……2分  …………4分 …………4分
∵ ……6分 ……6分 (2)由 ……8分 ……8分 ∴ ,故tanB=2 …………10分 ,故tanB=2 …………10分 18.解:(1)设取出的球不放回袋中,第3次取球才得到红球的概率为P1, 则 ………………6分 ………………6分 (2)设取出的球放回袋中,第3次取球才得到红球的概率P2, 则 ………………12分 ………………12分 19.(1)证明:∵底面ABCD是菱形,且∠ABC=60° ∴AB=AD=AC=a,在△PAB中,由PA2+AB2=2a=PB2得PA⊥AB, 同理得PA⊥AD, ∴PA⊥平面ABCD (2)作EG//PA交AD于G,由PA⊥平面ABCD知EG⊥平面ABCD, 作GH//AC于H,连结EH,则EH⊥AC,∴∠EHG为二面角的平面角 ……8分 ∵PE:ED=2:1, ∴EG= ,……10分 ,……10分 ∴ …………12分 …………12分 20.(本小题12分) 解:(Ⅰ)∵ , , ∴ 的公比为 的公比为 的等比数列 …………3分 的等比数列 …………3分 又n=1时, ……6分 ……6分 (Ⅱ)∵ …………8分 …………8分 ∴  …… ……  ……10分 ……10分 以上各式相加得: ] ]  …………12分 …………12分
21.(本小题12分) 解:(Ⅰ)由题意,设双曲线方程为  ……2分 ……2分 又 ,∴方程为 ,∴方程为 …4分 …4分 (Ⅱ)由消去y得 ……7分 ……7分 当k=2时得   
 ……10分 ……10分
当k=-2时同理得 
综上:∠MFN为直角. …………12分 22.解:(1) …………2分 …………2分 ∵ 上为单调函数,而 上为单调函数,而 不可能恒成立 不可能恒成立 所以 在 在 上恒成立, 上恒成立, ∴ …………6分 …………6分 (2)依题意,方程 有两个不同的实数根 有两个不同的实数根 , , 由 ……9分 ……9分 
 所以 

所以  综上: ………………12分 ………………12分
| | | | | |
