|
试题详情
试题详情
试题详情
10.将5本不同的书全发给4名同学,每名同学至少有一本书的分配方案有
种 试题详情
试题详情
12.已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的表面积为
试题详情
13.如果一条直线与一个平面平行,那么称此直线与平面构成一个“平行线面组”,在一个长方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行 线面组”的个数是
试题详情
试题详情
二、解答题:(文科班只做15题,30分,理科班两题都做,每题15分
|
试题详情
试题详情
(2)设 与圆 与圆 相交与两点 相交与两点 ,求点 ,求点 到 到 两点的距离之积. 两点的距离之积. 09届高三数学天天练18答案 试题详情
试题详情
试题详情
15.解: 连接BD交AC于O,则BD⊥AC, 连接A1O 在△AA1O中,AA1=2,AO=1, ∠A1AO=60° ∴A1O2=AA12+AO2-2AA1?Aocos60°=3 ∴AO2+A1O2=A12 ∴A1O⊥AO,由于平面AA1C1C⊥ 平面ABCD, 所以A1O⊥底面ABCD 试题详情
∴以OB.OC.OA1所在直线为x轴.y轴.z轴建立如图所示空间直角坐标系,则A(0,-1,0),B( ,0,0),C(0,1,0),D(- ,0,0),C(0,1,0),D(- ,0,0),A1(0,0, ,0,0),A1(0,0, ) ) ……………………2分 试题详情
(Ⅰ)由于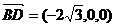 试题详情
试题详情
则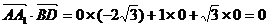 ∴BD⊥AA1……………………4分 (Ⅱ)由于OB⊥平面AA1C1C 试题详情
∴平面AA1C1C的法向量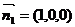 试题详情
设 ⊥平面AA1D ⊥平面AA1D 试题详情
则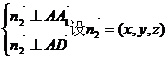 试题详情
得到 ……………………6分 ……………………6分 试题详情
试题详情
所以二面角D―A1A―C的平面角的余弦值是 ……………………8分 ……………………8分 (Ⅲ)假设在直线CC1上存在点P,使BP//平面DA1C1 试题详情
设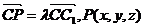 试题详情
则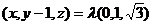 试题详情
得 ……………………9分 ……………………9分 试题详情
|
试题详情
设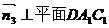 试题详情
则 设 设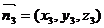 试题详情
得到 ……………………10分 ……………………10分 试题详情
又因为 平面DA1C1 平面DA1C1 试题详情
则 ? ?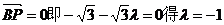 即点P在C1C的延长线上且使C1C=CP……………………12分 法二:在A1作A1O⊥AC于点O,由于平面AA1C1C⊥平面 ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD, 又底面为菱形,所以AC⊥BD 试题详情
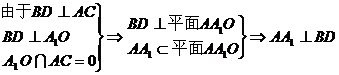
……………………4分 (Ⅱ)在△AA1O中,A1A=2,∠A1AO=60° ∴AO=AA1?cos60°=1 所以O是AC的中点,由于底面ABCD为菱形,所以 O也是BD中点 由(Ⅰ)可知DO⊥平面AA1C 过O作OE⊥AA1于E点,连接OE,则AA1⊥DE 则∠DEO为二面角D―AA1―C的平面角……………………6分 在菱形ABCD中,AB=2,∠ABC=60° ∴AC=AB=BC=2 试题详情
∴AO=1,DO=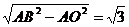 试题详情
在Rt△AEO中,OE=OA?sin∠EAO=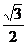 试题详情
DE=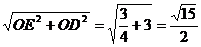 试题详情
∴cos∠DEO=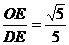 试题详情
∴二面角D―A1A―C的平面角的余弦值是 ……………………8分 ……………………8分 (Ⅲ)存在这样的点P 试题详情
连接B1C,因为A1B1 AB AB DC DC ∴四边形A1B1CD为平行四边形。 ∴A1D//B1C 在C1C的延长线上取点P,使C1C=CP,连接BP……………………10分 试题详情
因B1B CC1,……………………12分 CC1,……………………12分 试题详情
∴BB1 CP CP ∴四边形BB1CP为平行四边形 则BP//B1C ∴BP//A1D ∴BP//平面DA1C1 试题详情
16.(1)直线的参数方程为 ,即 ,即 . 5′ . 5′ 试题详情
(2)把直线 代入 代入 , , 试题详情
试题详情
| | | | |

 满足
满足 ,则
,则

 的离心率为
的离心率为 ,且它的一条准线与抛物线
,且它的一条准线与抛物线 的准线重合,则此双曲线的方程为
的准线重合,则此双曲线的方程为  4.已知变量
4.已知变量 满足约束条件
满足约束条件 ,则
,则 的取值范围是
的取值范围是  和平面
和平面 的四个命题:
的四个命题: ;
; 是异面直线,
是异面直线, ;
; ;
;
 化为十进制数的
化为十进制数的