
题目列表(包括答案和解析)
1. 轻绳
(1)轻绳模型的特点
“绳”在物理学上是个绝对柔软的物体,它只产生拉力(张力),绳的拉力沿着绳的方向并指向绳的收缩方向。它不能产生支持作用。
它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子方向的力。它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长。
(2)轻绳模型的规律
①轻绳各处受力相等,且拉力方向沿着绳子;
②轻绳不能伸长;
③用轻绳连接的系统通过轻绳的碰撞、撞击时,系统的机械能有损失;
④轻绳的弹力会发生突变。
7.
解:设滑块至B点时速度为vB,对滑块由A点到B点应用动能定理有
 …………2分
…………2分
解得  …………1分
…………1分
滑块从B点开始运动后机构能守恒,设滑块到达P处时速度为 ,则
,则
 …………2分
…………2分
解得  …………1分
…………1分
滑块穿过P孔后再回到平台的时间  …………2分
…………2分
要想实现题述过程,需满足  …………2分
…………2分
 (n=0,1,2……) …………2分
(n=0,1,2……) …………2分
6.
解:(1)设钢球的轨道M最高点的速度为v,在M的最低端速度为v0,则在最高点,
由题意得 ①(2分)
①(2分)
从最低点到最高点,由机械能守恒定律得: ②(3分)
②(3分)
由①②得: ③ (1分)
③ (1分)
设弹簧的弹性势能为 ,由机械能守恒定律得:
,由机械能守恒定律得:
 =1.5×10-1J ④
(2分)
=1.5×10-1J ④
(2分)
(2)钢珠从最高点飞出后,做平抛运动 ⑤ (1分)
⑤ (1分)
 ⑥ (2分)
⑥ (2分)
由几何关系 ⑦ (3分)
⑦ (3分)
联立⑤、⑥、⑦得t=0.24s (2分)
5.
(1)设弹簧压缩量为 时绳被拉断:
时绳被拉断:
从初始状态到压缩绳被拉断的过程中,
故细绳被拉断的条件为
(2)设绳被拉断瞬间,小物体的速度为 ,有
,有
解得
当弹簧压缩至最短时,滑块有向左的最大加速度 ,
,
此时,设弹簧压缩量为 ,小物体和滑块有相同的速度为
,小物体和滑块有相同的速度为
从绳被拉断后到弹簧压缩至最短时,小物体和滑块,弹簧系统的动量守恒,机械能守恒:


由牛顿第二定律:
解得
(3)设小物体离开时,滑块M速度为 ,有:
,有:
, ,解得
,解得
由于 ,故物体最后离开滑块时,相对地面速度恰好为零的条件是
,故物体最后离开滑块时,相对地面速度恰好为零的条件是
 ,且满足
,且满足
4.
解:
(1)设物体与斜面间的滑动摩擦因数为μ,则物体上滑由A到B做速度由v0变为0的匀减速运动,令加速度大小为a,
则由牛顿第二定律,可得mgsinθ+μmgcosθ=ma…①(2分),
又由运动学公式,可得0-v02=-2a·AB…②(1分),
由①、②式解得 (1分),代入数据可得μ=0.25(1分)。
(1分),代入数据可得μ=0.25(1分)。
(2)设物体返回经过C点时速度大小为v1,则对于物体由B到C,
由动能定理有 …③(2分),
…③(2分),
又 …④(1分),由③、④式解得
…④(1分),由③、④式解得 (1分),
(1分),
代入数据可得:h=0.24m(1分)
3.
解:
(1)小球恰能在A点沿轨道运动时:
 (2分)
(2分)
此时,小球在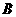 点动能最小,由机械能守恒:
点动能最小,由机械能守恒:
 (2分)
(2分)
解得:
 (1分)
(1分)
(2)在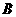 点:
点: (2分)
(2分)
在 点:
点: (2分)
(2分)
小球从A到B机械能守恒:
 (2分)
(2分)
两点的压力差: (1分)
(1分)
(3)由图象知:
截距:
 (2分)
(2分)
斜率:
 (2分)
(2分)
2.
解:(1)解除锁定,弹开物块AB后,两物体的速
度大小VA=vB= =4.0m/s
=4.0m/s
弹簧储存的弹性势能 J(2分)
J(2分)
(2)物块B滑上传送带做匀减速运动,当速度减为零时,滑动的距离最远。
由动能定理得 得 (3分)
(3)vB’=  = 4m/s(3分)
= 4m/s(3分)
1.解:(1)对小物块,由A到B有
 …………1分
…………1分
在B点 …………2分
…………2分
所以 …………1分
…………1分
(2)对小物块,由B到O有
 …………2分
…………2分
其中 …………1分
…………1分
在O点 …………1分
…………1分
所以N=43N
由牛顿第三定律知对轨道的压力为 …………1分
…………1分
(3)物块沿斜面上滑: …………1分
…………1分
所以
物块沿斜面上滑: …………1分
…………1分
由机械能守恒知
小物块由C上升到最高点历时 …………1分
…………1分
小物块由最高点回到D点历时 …………1分
…………1分
故 …………1分
…………1分
即 …………1分
…………1分
(4)小物块在传送带上加速过程: …………1分
…………1分
PA间的距离是 …………1分
…………1分
1 
1.D 2.B 3.ABC 4.BC 5.BCD 6.D 7.BD 8.BD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com