
题目列表(包括答案和解析)
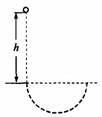
1.如图所示,质量为m、电荷量为q的带电液滴从h高处自由下落,进入一个互相垂直的匀强电场和匀强磁场区域,磁场方向垂直纸面,磁感应强度为B,电场强度为E.已知液滴在此区域中做匀速圆周运动,则圆周运动的半径R为( )
 A.
A.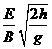 B.
B.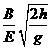
C.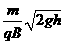 D.
D.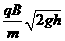
答案:AC
9.(石景山区2008--2009学年第一学期期末考试试卷)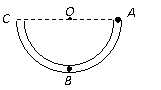 7.如图所示,在竖直放置的光滑半圆形绝缘细管的圆心O处放一点电荷.现将质量为m、电荷量为q的小球从半圆形管的水平直径端点A静止释放,小球沿细管滑到最低点B时,对管壁恰好无压力.若小球所带电量很小,不影响O点处的点电荷的电场,则置于圆心处的点电荷在B点处的电场强度的大小为:
7.如图所示,在竖直放置的光滑半圆形绝缘细管的圆心O处放一点电荷.现将质量为m、电荷量为q的小球从半圆形管的水平直径端点A静止释放,小球沿细管滑到最低点B时,对管壁恰好无压力.若小球所带电量很小,不影响O点处的点电荷的电场,则置于圆心处的点电荷在B点处的电场强度的大小为:
 A.
A.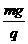 B.
B.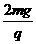 C.
C.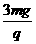 D.
D.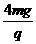
答案:C
8.(海淀区高三年级第一学期期末练习)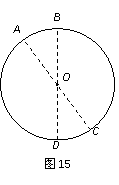 10. 如图15所示,BD是竖直平面上圆的一条竖直直径,AC是该圆的任意一条直径,已知AC和BD不重合,且该圆处于匀强电场中,场强大小为E,方向在圆周平面内。将一带负电的粒子Q从O点以相同的动能射出,射出方向不同时,粒子会经过圆周上不同的点,在这些所有的点中,到达A点时粒子的动量总是最小。如果不考虑重力作用的影响,则关于电场强度的下列说法中正确的是 ( )
10. 如图15所示,BD是竖直平面上圆的一条竖直直径,AC是该圆的任意一条直径,已知AC和BD不重合,且该圆处于匀强电场中,场强大小为E,方向在圆周平面内。将一带负电的粒子Q从O点以相同的动能射出,射出方向不同时,粒子会经过圆周上不同的点,在这些所有的点中,到达A点时粒子的动量总是最小。如果不考虑重力作用的影响,则关于电场强度的下列说法中正确的是 ( )
A.一定由C点指向A点 B.一定由A点指向C点
C.可能由B点指向D点? D.可能由D点指向B点
答案:A
7.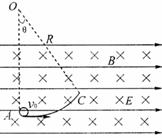 (丰台区2008-2009学年度第一学期期末考试)22.(14分)在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R = 1.8 m,OA连线在竖直方向上,AC弧对应的圆心角θ = 37°。今有一质量m = 3.6×10-4 kg、电荷量q = +9.0×10-4 C的带电小球(可视为质点),以v0 = 4.0 m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动。已知重力加速度g = 10 m/s2,sin37°
= 0.6,cos370=0.8,不计空气阻力,求:
(丰台区2008-2009学年度第一学期期末考试)22.(14分)在某空间存在着水平向右的匀强电场和垂直于纸面向里的匀强磁场,如图所示,一段光滑且绝缘的圆弧轨道AC固定在纸面内,其圆心为O点,半径R = 1.8 m,OA连线在竖直方向上,AC弧对应的圆心角θ = 37°。今有一质量m = 3.6×10-4 kg、电荷量q = +9.0×10-4 C的带电小球(可视为质点),以v0 = 4.0 m/s的初速度沿水平方向从A点射入圆弧轨道内,一段时间后从C点离开,小球离开C点后做匀速直线运动。已知重力加速度g = 10 m/s2,sin37°
= 0.6,cos370=0.8,不计空气阻力,求:
(1)匀强电场的场强E;
(2)小球射入圆弧轨道后的瞬间对轨道的压力。
解:
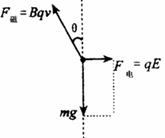 (1)当小球离开圆弧轨道后,对其受力分析如图所示,
(1)当小球离开圆弧轨道后,对其受力分析如图所示,
由平衡条件得:F电 = qE = mgtan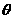 (2分)
(2分)
代入数据解得:E =3 N/C (1分)
(2)小球从进入圆弧轨道到离开圆弧轨道的过程中,由动能定理得:
F电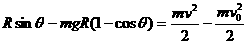 (2分)
(2分)
代入数据得: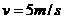 (1分)
(1分)
由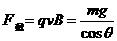 (2分)
(2分)
解得:B=1T (2分)
 分析小球射入圆弧轨道瞬间的受力情况如图所示,
分析小球射入圆弧轨道瞬间的受力情况如图所示,
由牛顿第二定律得: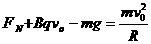 (2分)
(2分)
代入数据得: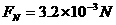 (1分)
(1分)
由牛顿第三定律得,小球对轨道的压力
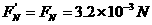 (1分)
(1分)
6.(北京市西城区2009年抽样测试)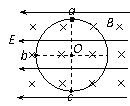 10.如图,空间存在水平向左的匀强电场和垂直纸面向里的匀强磁场,电场和磁场相互垂直。在电磁场区域中,有一个竖直放置的光滑绝缘圆环,环上套有一个带正电的小球。O点为圆环的圆心,a、b、c为圆环上的三个点,a点为最高点,c点为最低点,Ob沿水平方向。已知小球所受电场力与重力大小相等。现将小球从环的顶端a点由静止释放。下列判断正确的是
10.如图,空间存在水平向左的匀强电场和垂直纸面向里的匀强磁场,电场和磁场相互垂直。在电磁场区域中,有一个竖直放置的光滑绝缘圆环,环上套有一个带正电的小球。O点为圆环的圆心,a、b、c为圆环上的三个点,a点为最高点,c点为最低点,Ob沿水平方向。已知小球所受电场力与重力大小相等。现将小球从环的顶端a点由静止释放。下列判断正确的是
A.当小球运动的弧长为圆周长的1/4时,洛仑兹力最大
B.当小球运动的弧长为圆周长的1/2时,洛仑兹力最大
C.小球从a点到b点,重力势能减小,电势能增大
D.小球从b点运动到c点,电势能增大,动能先增大后减小
答案:D
5、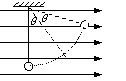 带电小球在场中A点处于平衡状态,此时线的张力T与等效重力mg’相平衡。
带电小球在场中A点处于平衡状态,此时线的张力T与等效重力mg’相平衡。
已知如图,匀强电场方向水平向右,场强E=1.5×106V/m,丝线长l=40cm,上端系于O点,下端系一质量为m=1.0×10-4kg,带电量为q=+4.9×10-10C的小球,将小球从最低点A由静止释放,求:⑴小球摆到最高点时丝线与竖直方向的夹角多大?⑵摆动过程中小球的最大速度是多大?
解:⑴这是个“歪单摆”。由已知电场力Fe=0.75G摆动到平衡位置时丝线与竖直方向成37°角,因此最大摆角为74°。
⑵小球通过平衡位置时速度最大。由动能定理:1.25mgž0.2l=mvB2/2,vB=1.4m/s。
思考:真空中存在空间范围足够大的、水平向右的匀强电场.在电场中,若将一个质量为m、带正电的小球由静止释放,运动中小球的速度与竖直方向夹角为37º(取sin37º=0.6,cos370=0.8).现将该小球从电场中某点以初速度v0竖直向上抛出.求运动过程中
⑴小球受到的电场力的大小和方向;
⑵小球从抛出点至最高点的电势能变化量;
⑶小球的最小动量的大小和方向.
(答案:⑴3mg/4,水平向右 ⑵9mv02/32 ⑶3mv0/5,与电场方向夹角为37º,斜向上.)
4、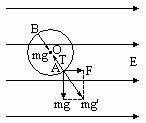 如图所示,一条长为L的绝缘细线上端固定,下端拴一质量为m的带电小球,将它置于水平方向的匀强电场中,场强为E,已知当细线与竖直方向的夹角为α时,小球处于平衡位置A点,问在平衡位置以多大的速度VA释放小球,刚能使之在电场中作竖直平面内的完整圆周运动?
如图所示,一条长为L的绝缘细线上端固定,下端拴一质量为m的带电小球,将它置于水平方向的匀强电场中,场强为E,已知当细线与竖直方向的夹角为α时,小球处于平衡位置A点,问在平衡位置以多大的速度VA释放小球,刚能使之在电场中作竖直平面内的完整圆周运动?
解:小球受重力mg、电场力Eq、线的拉力T作用。简化处理,将复合场(重力场和电场)等效为重力场,小球在等效重力场中所受重力为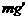 ,由图有:
,由图有:
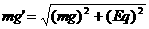 , 即
, 即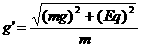
小球在A点处于平衡状态,若小球在A点以速度VA开始绕O点在竖直平面内作圆周运动,若能通过延长线上的B点(等效最高点)就能做完整的圆周运动,在B点根据向心力公式得: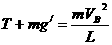 。
。
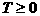 为临界条件,所以
为临界条件,所以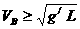
又因仅重力、电场力对小球做功,由动能定理得: 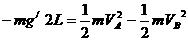
由以上二式解得: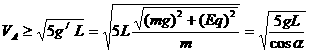 。
。
3、如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,已知球B运动到最高点时,球B对杆恰好无作用力.求:
(1)球B在最高点时,杆对水平轴的作用力大小.
(2)球B转到最低点时,球A和球B对杆的作用力分别是多大?方向如何?
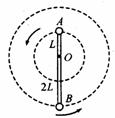
解析:(1)球B在最高点时速度为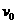 ,有
,有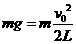 ,得
,得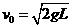
此时球A的速度为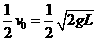 ,设此时杆对球A的作用力为
,设此时杆对球A的作用力为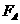 ,则
,则
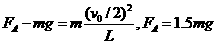
A球对杆的作用力为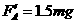
水平轴对杆的作用力与A球对杆的作用力平衡,再据牛顿第三定律知,杆对水平轴的作用力大小为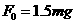
(2)设球B在最低点时的速度为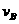 ,取O点为参考平面,据机械能守恒定律有
,取O点为参考平面,据机械能守恒定律有
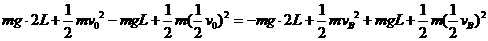
解得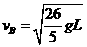
对A球有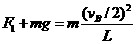
解得杆对A球的作用力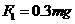
对B球有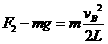
解得杆对B球的作用力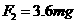
据牛顿第三定律可知,A球对杆的作用力大小为0. 3 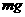 ,方向向上;B对杆的作用力大小为3. 6
,方向向上;B对杆的作用力大小为3. 6  ,方向向下.
,方向向下.
2、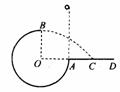 如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R,A端与圆心O等高,AD为水平面,B点在O的正上方,一个小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰能到达B点.求:
如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R,A端与圆心O等高,AD为水平面,B点在O的正上方,一个小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰能到达B点.求:
(1)释放点距A点的竖直商度,
(2)落点C与A点的水平距离.
解析:(1)释放点到A高度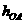 ,则
,则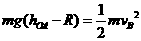
恰能通过最高点B,有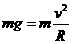 ,
,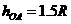
(2)由B到C小球做平抛运动,有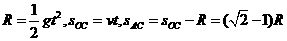
1、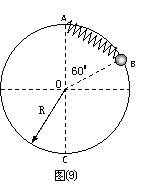 (湘钢一中2009届10月月考试题).如图⑼所示,一个质量为m=0.20kg的小球系于轻质弹簧的一端,且套在竖直固定的光滑圆环上,弹簧的另一端固定于环的最高点A ,环的半径R=0.50m 。弹簧原长LO=0.50m,劲度系数k=4.8N/m 。若小球从图中的B位置由静止开始滑到环的最低点C时,弹簧的弹性势能EP =0.60J。求:
(湘钢一中2009届10月月考试题).如图⑼所示,一个质量为m=0.20kg的小球系于轻质弹簧的一端,且套在竖直固定的光滑圆环上,弹簧的另一端固定于环的最高点A ,环的半径R=0.50m 。弹簧原长LO=0.50m,劲度系数k=4.8N/m 。若小球从图中的B位置由静止开始滑到环的最低点C时,弹簧的弹性势能EP =0.60J。求:
⑴小球经过C点时的速度vC=?
⑵小球经过C点时对环的压力(g=10m/s2)
.(1)3m/s (2) 3.2N
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com