
题目列表(包括答案和解析)
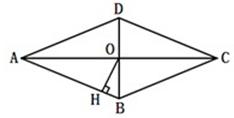
14、(2011•綦江县)如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点0到边AB的距离OH=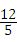 .
.
考点:菱形的性质;点到直线的距离;勾股定理。
分析:因为菱形的对角线互相垂直平分,菱形的四边相等,根据面积相等,可求出OH的长.
解答:解:∵AC=8,BD=6,
∴BO=3,AO=4,
∴AB=5.
 AO•BO=
AO•BO= AB•OH,
AB•OH,
OH=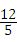 .
.
故答案为: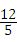 .
.
点评:本题考查菱形的基本性质,菱形的对角线互相垂直平分,菱形的四边相等,根据面积相等,可求出AB边上的高OH.
13、(2011•綦江县)如图,已知AB为⊙O的直径,∠CAB=30°,则∠D= 60° .
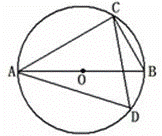
考点:圆周角定理。
专题:计算题。
分析:首先利用直径所对的圆周角是直角得到直角三角形,然后求得另一锐角的度数,从而求得所求的角.
解答:解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=30°,
∴∠B=60°,
∴∠D=60°,
故答案为:60°.
点评:本题考查了圆周角定理,解决本题的关键是利用直径所对的圆周角是直角得到直角三角形.
12、(2011•綦江县)若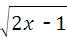 有意义,则x的取值范围是 x≥
有意义,则x的取值范围是 x≥ .
.
考点:二次根式有意义的条件。
分析:根据二次根式的定义可知被开方数必须为非负数,列不等式求解.
解答:解:要是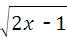 有意义,
有意义,
则2x﹣1≥0,
解得x≥ .
.
故答案为:x≥ .
.
点评:本题主要考查了二次根式有意义的条件,二次根式中的被开方数必须是非负数,否则二次根式无意义.
11、(2011•綦江县)经过倾力打造,綦江旅游业得到一定发展,到綦江旅游的人数逐年增加.据旅游部门统计今年上半年到我县古剑山、丁山湖、东溪古镇,永新梨花山等景点旅游的人数已达63700人,这个数用科学记数法表示为 6.37×104.
考点:科学记数法-表示较大的数。
分析:先根据科学记数法的概念求出n的值,再用科学记数法表示即可.
解答:解:∵63700共有5位数,
∴n=5﹣1=4,
∴63700用科学记数法表示为:6.37×104.
故答案为:6.37×104.
点评:本题考查的是科学记数法的概念,即把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n是正整数,这种记数法叫做科学记数法.
10、(2011•綦江县)如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中 所填整数之和都相等,则第2011个格子中的数为( )
|
3 |
a |
b |
c |
﹣1 |
|
|
|
2 |
|
… |
A、3 B、2
C、0 D、﹣1
考点:规律型:数字的变化类。
专题:规律型。
分析:首先由已知和表求出a、b、c,再观察找出规律求出第2011个格子中的数.
解答:解:已知其中任意三个相邻格子中 所填整数之和都相等,
则,3+a+b=a+b+c,a+b+c=b+c﹣1,
所以a=﹣1,c=3,
按要求排列顺序为,3,﹣1,b,3,﹣1,b,…,
再结合已知表得:b=2,
所以每个小格子中都填入一个整数后排列是:
3,﹣1,2,3,﹣1,2,…,
得到:每3个数一个循环,
则:2011÷3=670余1,
因此第2011个格子中的数为3.
故选A.
点评:此题考查的是数字的变化类问题,解题的关键是先由已知求出a、b、c,再找出规律求出答案.
9、(2011•綦江县)小明从家中出发,到离家1.2千米的早餐店吃早餐,用了一刻钟吃完早餐后,按原路返回到离家1千米的学校上课,在下列图象中,能反映这一过程的大致图象是( )
A、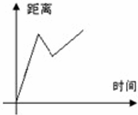 B、
B、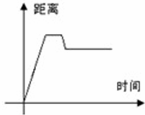
C、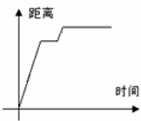 D、
D、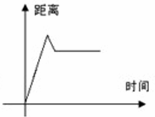
考点:函数的图象。
分析:首先分析题干条件,小明从家中出发,到离家1.2千米的早餐店吃早餐,用了一刻钟吃完早餐后,据此可以判断A和D错误,然后小明原路返回到离家1千米的学校上课,即学校在家和早餐店之间,依次可以可到答案.
解答:解:小明从家中出发,到离家1.2千米的早餐店吃早餐,距离逐渐增大,当吃早餐时,距离不变,当返回学校时,距离变大,到达学校距离不再变化.
故选C.
点评:本题主要考查函数的图象的知识点,解答本题的关键是理解原路返回到离家1千米的学校上课这句话得意思,也就是说学校在家和早餐店之间.
8、(2011•綦江县)在实施“中小学生蛋奶工程”中,某配送公司按上级要求,每周向学校配送鸡蛋10000 个,鸡蛋用甲、乙两种不同规格的包装箱进行包装,若单独使用甲型包装箱比单独使用 乙型包装箱可少用10个,每个甲型包装箱比每个乙型包装箱可多装50个鸡蛋,设每个 甲型包装箱可装x个鸡蛋,根据题意下列方程正确的是( )
A、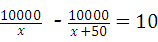 B、
B、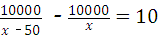
C、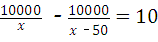 D、
D、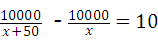
考点:由实际问题抽象出分式方程。
分析:设每个甲型包装箱可装x个鸡蛋,根据若单独使用甲型包装箱比单独使用 乙型包装箱可少用10个,每个甲型包装箱比每个乙型包装箱可多装50个鸡蛋,可列出分式方程.
解答:解:设每个甲型包装箱可装x个鸡蛋,
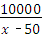 ﹣
﹣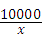 =10.
=10.
故选B.
点评:本题考查理解题意能力,以包装箱个数做为等量关系,根据若单独使用甲型包装箱比单独使用 乙型包装箱可少用10个,每个甲型包装箱比每个乙型包装箱可多装50个鸡蛋,可列方程求解.
7、(2011•綦江县)如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,0A=3,那么∠AOB所对弧的长度为( )
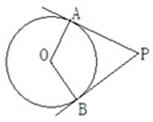
A、6π B、5π
C、3π D、2π
考点:弧长的计算;切线的性质。
专题:计算题。
分析:由于PA、PB是⊙O的切线,由此得到∠OAP=∠OBP=90°,而∠P=60°,然后利用四边形的内角和即可求出∠AOB然后利用已知条件和弧长公式即可求出∠AOB所对弧的长度.
解答:解:∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
而∠P=60°,
∴∠AOB=120°,
∠AOB所对弧的长度=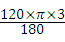 =2π.
=2π.
故选D.
点评:此题主要考查了弧长的计算问题,也利用了切线的性质和四边形的内角和,题目简单.
86、87、88、92、92.
最中间的年龄是88,
故中位数是88.
故选:C.
点评:此题主要考查了中位数的概念以及平均数的求法,根据中位数定义给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数,熟练记忆定义是解决问题的关键.
6、(2011•綦江县)在“庆祝建党90周年的红歌传唱活动”比寒中,七位评委给某参赛队打的分数为:92、86、88、87、92、94、86,则去掉一个最高分和一个最低分后,所剩五个分数的平均数和中位数是( )
A、89,92 B、87,88
C、89,88 D、88,92
考点:中位数;算术平均数。
专题:计算题。
分析:要求平均数只要求出数据之和再除以总个数即可;求中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.
解答:解:根据去掉一个最高分和一个最低分后,所剩五个分数的平均数为:
平均数:(92+86+88+87+92)÷5=89,故平均数是89;
将数据按从小到大的顺序排列得:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com