13、(2011•江津区)在梯形ABCD中，AD∥BC，中位线长为5，高为6，则它的面积是　30　．

考点：梯形中位线定理。

专题：计算题。

分析：利用梯形的中位线的定义求得两底和，在利用梯形的面积计算方法计算即可．

解答：解：∵中位线长为5，

∴AD+BC=2×5=10，

∴梯形的面积为：，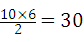

故答案为30．

点评：本题考查的知识比较全面，需要用到梯形和三角形中位线定理以及平行四边形的性质．

12、(2011•江津区)分解因式：2x3﹣x2=　x2(2x﹣1)　．

考点：因式分解-提公因式法。

专题：因式分解。

分析：观察等式的右边，提取公因式x2即可求得答案．

解答：解：2x3﹣x2=x2(2x﹣1)．

故答案为：x2(2x﹣1)．

点评：此题考查了提公因式法分解因式．解题的关键是准确找到公因式．

11、(2011•江津区)今年长江中下游旱情严重，某地村民吃水都成问题，一消防大队决定支援灾区，为灾区人民送去饮用水13万吨，用科学记数法表示为　1.3×105吨．

考点：科学记数法-表示较大的数。

专题：计算题。

分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

解答：解：将13万用科学记数法表示为1.3×105．

故答案为：1.3×105．

点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

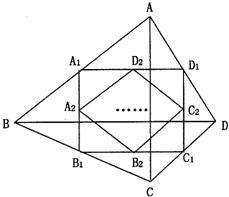
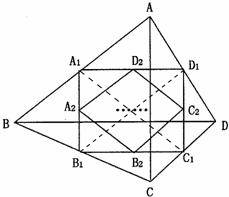
10、(2011•江津区)如图，四边形ABCD中，AC=a，BD=b，且AC丄BD，顺次连接四边形ABCD 各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2…，如此进行下去，得到四边形AnBnCnDn．下列结论正确的有(　)

①四边形A2B2C2D2是矩形；

②四边形A4B4C4D4是菱形；

③四边形A5B5C5D5的周长是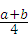

④四边形AnBnCnDn的面积是．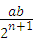

　　 A、①②　　 B、②③

　　 C、②③④　　　 D、①②③④

考点：三角形中位线定理；菱形的判定与性质；矩形的判定与性质。

专题：规律型。

分析：首先根据题意，找出变化后的四边形的边长与四边形ABCD中各边长的长度关系规律，然后对以下选项作出分析与判断：

①根据矩形的判定与性质作出判断；

②根据菱形的判定与性质作出判断；

③由四边形的周长公式：周长=边长之和，来计算四边形A5B5C5D5的周长；

④根据四边形AnBnCnDn的面积与四边形ABCD的面积间的数量关系来求其面积．

解答：解：①连接A1C1，B1D1．

∵在四边形ABCD中，顺次连接四边形ABCD 各边中点，得到四边形A1B1C1D1，

∴A1D1∥BD，B1C1∥BD，C1D1∥AC，A1B1∥AC；

∴A1D1∥B1C1，A1B1∥C1D1，

∴四边形ABCD是平行四边形；

∴B1D1=A1C1(平行四边形的两条对角线相等)；

∴A2D2=C2D2=C2B2=B2A2(中位线定理)，

∴四边形A2B2C2D2是菱形；

故本选项错误；

②由①知，四边形A2B2C2D2是菱形；

∴根据中位线定理知，四边形A4B4C4D4是菱形；

故本选项正确；

③根据中位线的性质易知，A5B5=A3B3=×A1B1=××AB，B5C5=B3C3=×B1C1=××BC，

∴四边形A5B5C5D5的周长是2×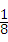(a+b)=；

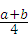故本选项正确；

④∵四边形ABCD中，AC=a，BD=b，且AC丄BD，

∴S四边形ABCD=ab；

由三角形的中位线的性质可以推知，每得到一次四边形，它的面积变为原来的一半，

四边形AnBnCnDn的面积是；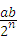

故本选项错误；

综上所述，②③④正确；

故选C．

点评：本题主要考查了菱形的判定与性质、矩形的判定与性质及三角形的中位线定理(三角形的中位线平行于第三边且等于第三边的一半)．解答此题时，需理清菱形、矩形与平行四边形的关系．

9、(2011•江津区)已知关于x的一元二次方程(a﹣l)x2﹣2x+l=0有两个不相等的实数根，则a的取值范围是(　)

　　 A、a＜2　　 B、a＞2

　　 C、a＜2且a≠l　　　 D、a＜﹣2

考点：根的判别式。

专题：计算题。

分析：利用一元二次方程根的判别式列不等式，解不等式求出a的取值范围．

解答：解：△=4﹣4(a﹣1)

=8﹣4a＞0

得：a＜2．

又a﹣1≠0

∴a＜2且a≠1．

故选C．

点评：本题考查的是一元二次方程根的判别式，根据方程有两不等的实数根，得到判别式大于零，求出a的取值范围，同时方程是一元二次方程，二次项系数不为零．

8、(2011•江津区)已知如图：(1)、(2)中各有两个三角形，其边长和角的度数已在图上标注，图(2)中AB、CD交于0点，对于各图中的两个三角形而言，下列说法正确的是(　)

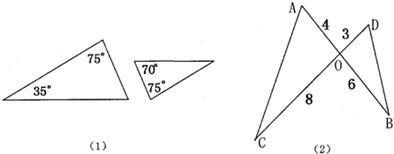
　　 A、都相似　　　 B、都不相似

　　 C、只有(1)相似　　　　 D、只有(2)相似

考点：相似三角形的判定。

分析：图(1)根据三角形的内角和定理，即可求得△ABC的第三角，由有两角对应相等的三角形相似，即可判定(1)中的两个三角形相似；

图(2)根据图形中的已知条件，即可证得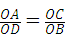，又由对顶角相等，即可根据对应边成比例且夹角相等的三角形相似证得相似．

解答：解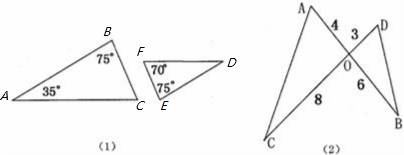：如图(1)∵∠A=35°，∠B=75°，

∴∠C=180°﹣∠A﹣∠B=70°，

∵∠E=75°，∠F=70°，

∴∠B=∠E，∠C=∠F，

∴△ABC∽△DEF；

如图(2)∵OA=4，OD=3，OC=8，OB=6，

∴，

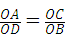∵∠AOC=∠DOB，

∴△AOC∽△DOB．

故选A．

点评：此题考查了相似三角形的判定．注意有两角对应相等的三角形相似与对顶角相等，即可根据对应边成比例且夹角相等的三角形相似的定理的应用．

7、(2011•江津区)某课外学习小组有5人，在一次数学测验中的成绩分别是：120，100，135，100，125，则他们的成绩的平均数和众数分别是(　)

　　 A、116和100　　　　 B、116和125

　　 C、106和120　　　　 D、106和135

考点：众数；中位数。

分析：众数的定义求解；众数是一组数据中出现次数最多的数据，注意众数可以不止一个；再利用平均数的求法得出答案．

解答：解：在这一组数据中100是出现次数最多的，故众数是100；

他们的成绩的平均数为：(120+100+135+100+125)÷5=116．

故选A．

点评：此题主要考查了众数以及平均数的求法，此题比较简单注意计算时要认真减少不必要的计算错误．

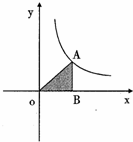
6、(2011•江津区)已知如图，A是反比例函数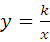的图象上的一点，AB丄x轴于点B，且△ABO的面积是3，则k的值是(　)

　　 A、3　　　　 B、﹣3

　　 C、6　　　　 D、﹣6

考点：反比例函数系数k的几何意义。

分析：过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S=|k|．

解答：解：根据题意可知：S△AOB=|k|=3，

又反比例函数的图象位于第一象限，k＞0，

则k=6．

故选C．

点评：本题主要考查了反比例函数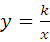中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得三角形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．

5、(2011•江津区)下列说法不正确是(　)

　　 A、两直线平行，同位角相等　　　 B、两点之间直线最短

　　 C、对顶角相等　　　 D、半圆所对的圆周角是直角

考点：圆周角定理；线段的性质：两点之间线段最短；对顶角、邻补角；平行线的性质。

专题：常规题型。

分析：利用平行线的性质可以判断A；利用线段公理可以判断B；利用对顶角的性质可以判断C；利用圆周角定理可以判断D．

解答：解：A、由平行线的性质可以得到本选项正确；

B、∵两点之间线段最短，

∴两点之间直线最短错误，故本选项错误；

C、利用对顶角的性质可以判断本选项C正确；

D、∵半圆或直径所对的圆周角是直角，正确．

故选B．

点评：本题考查了圆周角定理及对顶角、邻补角及平行线的性质，是一道综合考查几何定理或概念的基础题，难度较小．

4、(2011•江津区)直线y=x﹣1的图象经过的象限是(　)

　　 A、第一、二、三象限　　 B、第一、二、四象限

　　 C、第二、三、四象限　　 D、第一、三、四象限

考点：一次函数的性质。

专题：计算题。

分析：由y=x﹣1可知直线与y轴交于(0，﹣1)点，且y随x的增大而增大，可判断直线所经过的象限．

解答：解：直线y=x﹣1与y轴交于(0，﹣1)点，

且k=1＞0，y随x的增大而增大，

∴直线y=x﹣1的图象经过第一、三、四象限．

故选D．

点评：本题考查了一次函数的性质．关键是根据图象与y轴的交点位置，函数的增减性判断图象经过的象限．